NO.PZ2020010801000009
问题如下:
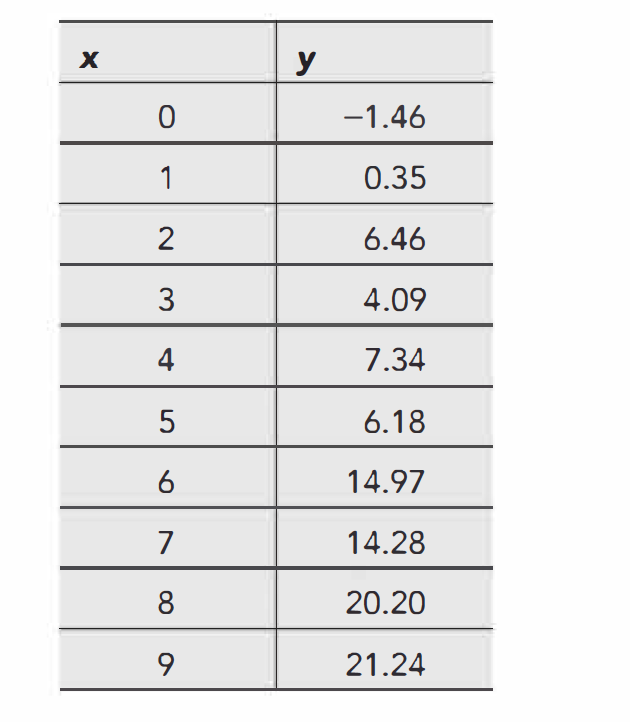
Find the OLS estimators for the following data:
选项:
解释:
Doing the basic needed calculations:
是不是上下各除以了一个n然后抵消了?
NO.PZ2020010801000009问题如下Finthe OLS estimators for the following t ing the basic neecalculations: β^=∑(Xi−X‾)(Yi−Y‾)∑(Xi−X‾)2=20.69/8.25=2.508\wihat\beta = \frac{\sum (X_i-\overline X)(Y_i-\overline Y)}{\sum (X_i-\overline X)^2}=20.69/8.25=2.508β=∑(Xi−X)2∑(Xi−X)(Yi−Y)=20.69/8.25=2.508α^=Y‾−β^X‾=9.365−2.508∗4.5=−1.921\wihat\alpha = \overline Y-\wihat\beta \overline X=9.365-2.508*4.5=-1.921α=Y−βX=9.365−2.508∗4.5=−1.921 老师,这道题用计算 2n7 分别输入X和Y的值,再按2n8,选lin,一直按向下的箭头,得出a=-2.886279,b=2.631779。和答案完全不一样,是哪里错了吗
NO.PZ2020010801000009 问题如下 Finthe OLS estimators for the following t ing the basic neecalculations: β^=∑(Xi−X‾)(Yi−Y‾)∑(Xi−X‾)2=20.69/8.25=2.508\wihat\beta = \frac{\sum (X_i-\overline X)(Y_i-\overline Y)}{\sum (X_i-\overline X)^2}=20.69/8.25=2.508β=∑(Xi−X)2∑(Xi−X)(Yi−Y)=20.69/8.25=2.508α^=Y‾−β^X‾=9.365−2.508∗4.5=−1.921\wihat\alpha = \overline Y-\wihat\beta \overline X=9.365-2.508*4.5=-1.921α=Y−βX=9.365−2.508∗4.5=−1.921 看了计算器基础课,讲了怎么录入两组变量值和基本统计数值的计算请问计算器能直接带出来这题要求的答案吗如果不能, 输入两组变量后, 计算器最多能算到哪一步呢
NO.PZ2020010801000009问题如下Finthe OLS estimators for the following t ing the basic neecalculations: β^=∑(Xi−X‾)(Yi−Y‾)∑(Xi−X‾)2=20.69/8.25=2.508\wihat\beta = \frac{\sum (X_i-\overline X)(Y_i-\overline Y)}{\sum (X_i-\overline X)^2}=20.69/8.25=2.508β=∑(Xi−X)2∑(Xi−X)(Yi−Y)=20.69/8.25=2.508α^=Y‾−β^X‾=9.365−2.508∗4.5=−1.921\wihat\alpha = \overline Y-\wihat\beta \overline X=9.365-2.508*4.5=-1.921α=Y−βX=9.365−2.508∗4.5=−1.921 想问一下 考试会出需要算这么多的题吗
NO.PZ2020010801000009问题如下Finthe OLS estimators for the following t ing the basic neecalculations: β^=∑(Xi−X‾)(Yi−Y‾)∑(Xi−X‾)2=20.69/8.25=2.508\wihat\beta = \frac{\sum (X_i-\overline X)(Y_i-\overline Y)}{\sum (X_i-\overline X)^2}=20.69/8.25=2.508β=∑(Xi−X)2∑(Xi−X)(Yi−Y)=20.69/8.25=2.508α^=Y‾−β^X‾=9.365−2.508∗4.5=−1.921\wihat\alpha = \overline Y-\wihat\beta \overline X=9.365-2.508*4.5=-1.921α=Y−βX=9.365−2.508∗4.5=−1.921 有x和y两组数据,请问为什么不能通过直接按计算器得到a和b呢?
NO.PZ2020010801000009 问题如下 Finthe OLS estimators for the following t ing the basic neecalculations: β^=∑(Xi−X‾)(Yi−Y‾)∑(Xi−X‾)2=20.69/8.25=2.508\wihat\beta = \frac{\sum (X_i-\overline X)(Y_i-\overline Y)}{\sum (X_i-\overline X)^2}=20.69/8.25=2.508β=∑(Xi−X)2∑(Xi−X)(Yi−Y)=20.69/8.25=2.508α^=Y‾−β^X‾=9.365−2.508∗4.5=−1.921\wihat\alpha = \overline Y-\wihat\beta \overline X=9.365-2.508*4.5=-1.921α=Y−βX=9.365−2.508∗4.5=−1.921 老师在强化班的课程里提到OLS ESTINATORS这块时好像说主要掌握性质,所以像本题这样的计算是否有很大必要花时间去掌握呢?