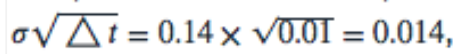开发者:上海品职教育科技有限公司 隐私政策详情

应用版本:4.2.11(IOS)｜3.2.5(安卓)APP下载

返回

Murasaki · 2021年09月23日

drift term的计算不懂

  1. FRM I
  2. Quantitative

NO.PZ2016062402000027

问题如下：

Suppose you simulate the price path of stock HHF using a geometric Brownian motion model with drift μ = 0, volatility σ = 0.14, and time step Δ = 0.01. Let StS_t be the price of the stock at time t. If S0S_0 = 100, and the first two simulated (randomly selected) standard normal variables are ε1\varepsilon_1 = 0.263 and ε2\varepsilon_2 = -0.475, what is the simulated stock price after the second step?

选项：

A.

96.79

B.

99.79

C.

99.97

D.

99.70

解释：

The process for the stock prices has mean of zero and volatility of σ△t=0.14×0.01=0.014\sigma\sqrt{\bigtriangleup t}=0.14\times\sqrt{0.01}=0.014, Hence the first step is S1=S0(1+0.014×0.263)=100.37S_1=S_0{(1+0.014\times0.263)}=100.37. The second step is S2=S1(1+0.014×−0.475)=99.70S_2=S_1{(1+0.014\times-0.475)}=99.70

drift term的计算不懂，题目中给的0，为啥计算机过程中显示1？

添加评论
1 个答案
已采纳答案

DD仔_品职助教 · 2021年09月23日

嗨，努力学习的PZer你好：


同学你好~

drift term是0，所以drift那一部分答案写的就是等于0的。

这个是公式：

dz=σ*ε

答案写的是：


也只有后面包含波动率的这一部分。


题目计算里写的1其实是把公式整合了

S1=S0+dS0=S0+S0*σ*dz=S0*（1+0.014*ε1）

S2计算同理也是整合的

----------------------------------------------
虽然现在很辛苦，但努力过的感觉真的很好，加油！

  • 1

    回答

  • 0

    关注

  • 1413

    浏览
相关问题

NO.PZ2016062402000027问题如下 Suppose you simulate the pripath of stoHHF using a geometric Brownimotion mol with ift μ = 0, volatility σ = 0.14, antime step Δ = 0.01. Let StS_tSt​ the priof the stotime t. If S0S_0S0​ = 100, anthe first two simulate(ranmly selecte stanrnormvariables are ε1\varepsilon_1ε1​ = 0.263 anε2\varepsilon_2ε2​ = -0.475, whis the simulatestopriafter the seconstep?96.79 99.79 99.97 99.70 The process for the stoprices hmeof zero anvolatility of σ△t=0.14×0.01=0.014\sigma\sqrt{\bigtriangleup t}=0.14\times\sqrt{0.01}=0.014σ△t​=0.14×0.01​=0.014, Henthe first step is S1=S0(1+0.014×0.263)=100.37S_1=S_0{(1+0.014\times0.263)}=100.37S1​=S0​(1+0.014×0.263)=100.37. The seconstep is S2=S1(1+0.014×−0.475)=99.70S_2=S_1{(1+0.014\times-0.475)}=99.70S2​=S1​(1+0.014×−0.475)=99.70请问这道题是哪个知识点

2022-11-18 15:22 4 · 回答

NO.PZ2016062402000027问题如下Suppose you simulate the pripath of stoHHF using a geometric Brownimotion mol with ift μ = 0, volatility σ = 0.14, antime step Δ = 0.01. Let StS_tSt​ the priof the stotime t. If S0S_0S0​ = 100, anthe first two simulate(ranmly selecte stanrnormvariables are ε1\varepsilon_1ε1​ = 0.263 anε2\varepsilon_2ε2​ = -0.475, whis the simulatestopriafter the seconstep? 96.79 99.79 99.97 99.70 The process for the stoprices hmeof zero anvolatility of σ△t=0.14×0.01=0.014\sigma\sqrt{\bigtriangleup t}=0.14\times\sqrt{0.01}=0.014σ△t​=0.14×0.01​=0.014, Henthe first step is S1=S0(1+0.014×0.263)=100.37S_1=S_0{(1+0.014\times0.263)}=100.37S1​=S0​(1+0.014×0.263)=100.37. The seconstep is S2=S1(1+0.014×−0.475)=99.70S_2=S_1{(1+0.014\times-0.475)}=99.70S2​=S1​(1+0.014×−0.475)=99.70 老师您好，如果u不等于0，怎么求？t = u*S*+Starviation * St*

2022-04-14 02:13 1 · 回答

请问，本题中的波动率是什么时间跨度？t=0.01是什么时间跨度？

2019-09-20 22:38 1 · 回答

有对应的课件页数和截图吗？没找到呀

2019-04-14 21:46 1 · 回答