NO.PZ2020011101000010
问题如下:
In the covariance-stationary AR(2), , where , what is the long-run mean and variance ?
解释:
Because this process is covariance-stationary
请问rho怎么计算的,谢谢
李坏_品职助教 · 2021年09月23日
嗨,从没放弃的小努力你好:
这个题目求的是mean和variance。
Yt是cov-stationary的,所以可以直接按照均值的公式计算long run mean和variance。
可以参考Notes里面的讲解:

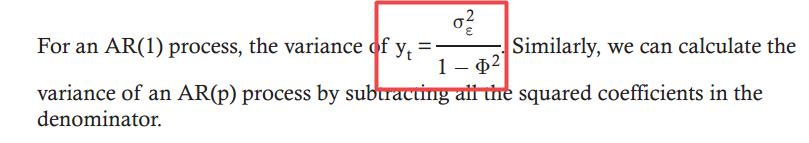
这个地方的φ,指的是模型里面的Y_t-1和Y_t-2的系数。
----------------------------------------------
虽然现在很辛苦,但努力过的感觉真的很好,加油!
nanaluo · 2021年09月23日
这个方差的公式是AR(1)的,怎么将基础班讲义264页求AR(p)的方差的公式跟题目答案关联起来?
NO.PZ2020011101000010 问题如下 In the covariance-stationary AR(2), Yt=0.3+1.4Yt−1−0.6Yt−2+ϵtY_t = 0.3 + 1.4Y_{t - 1} - 0.6Y_{t - 2} + \epsilon_tYt=0.3+1.4Yt−1−0.6Yt−2+ϵt, where ϵt∼WN(0,σ2)\epsilon_t ∼ WN(0, \sigma^2)ϵt∼WN(0,σ2), whis the long-run meE[Yt]E[Y_t]E[Yt] anvarianV[Yt]V[Y_t]V[Yt]? Because this process is covariance-stationary E[Yt]=μ=0.31−1.4−(−0.6)=1.5E[Y_t]=\mu=\frac{0.3}{1-1.4-(-0.6)}=1.5E[Yt]=μ=1−1.4−(−0.6)0.3=1.5V[Yt]=γ0=0.321−1.4−(−0.6)=0.45V[Y_t]=\gamma_0=\frac{0.3^2}{1-1.4-(-0.6)}=0.45V[Yt]=γ0=1−1.4−(−0.6)0.32=0.45 这里yt的系数 1,那么这个AR模型还是协方差平稳么?
NO.PZ2020011101000010问题如下 In the covariance-stationary AR(2), Yt=0.3+1.4Yt−1−0.6Yt−2+ϵtY_t = 0.3 + 1.4Y_{t - 1} - 0.6Y_{t - 2} + \epsilon_tYt=0.3+1.4Yt−1−0.6Yt−2+ϵt, where ϵt∼WN(0,σ2)\epsilon_t ∼ WN(0, \sigma^2)ϵt∼WN(0,σ2), whis the long-run meE[Yt]E[Y_t]E[Yt] anvarianV[Yt]V[Y_t]V[Yt]? Because this process is covariance-stationary E[Yt]=μ=0.31−1.4−(−0.6)=1.5E[Y_t]=\mu=\frac{0.3}{1-1.4-(-0.6)}=1.5E[Yt]=μ=1−1.4−(−0.6)0.3=1.5V[Yt]=γ0=0.321−1.4−(−0.6)=0.45V[Y_t]=\gamma_0=\frac{0.3^2}{1-1.4-(-0.6)}=0.45V[Yt]=γ0=1−1.4−(−0.6)0.32=0.45 老师好,e的方差为什么是0.3的平方?还有分母为什么不是1-Yt-1系数的平方-Yt—2系数的平方?
NO.PZ2020011101000010 分母是1-1.4和0.6的平方吗?
重新编写此题吧