丁洁Amy · 2021年08月25日
老师好，
原题如下：
题目涉及求date3这个时间点的coupon，其中，coupon rate = discount rate + 4%，par=1000。我看到答案解析的做法是先计算出date2的coupon rate，分别是8.3999%，6.9493%和5.977%。然后用83.999*0.25+69.493*0.5+59.77*0.25(以date2那一刻的概率)算出了加权平均到date3的coupon，得到70.6888。
我的做法是因为83.999、69.493、59.77分别以0.5的概率一拆二拆到了date3，所以我的公式是（83.999/2）*0.125+（83.999/2+69.493/2）*0.375+（69.493/2+59.77/2）*0.375+（59.77/2）*0.125，得到62.0021。
我算了两遍应该没算错，老师麻烦您帮我看看我的思路哪里错了？还有就是答案解析的思路我明白是怎么算的但是我不理解，希望老师帮我讲讲，谢谢老师！
WallE_品职答疑助手 · 2021年08月26日
嗨，从没放弃的小努力你好：
我看了下面的正确答案好几遍，实在是没理解同学你算“83.999*0.25+69.493*0.5+59.77*0.25” 或者"（83.999/2）*0.125+（83.999/2+69.493/2）*0.375+（69.493/2+59.77/2）*0.375+（59.77/2）*0.125" 的意思
每个节点的coupon rate和value都是独有的，需要你加起来在折现求前一个date的value.
您把coupon rate加权平均算出来是想表达什么呢？而且答案里面也没有像你说的这么去计算啊，70.6888您是在哪里找到的？
这一题是原版书课后题Reding 35的第11题，建议同学去听一下讲解，感觉同学还没有掌握这里的解题思路。
--------------------------------
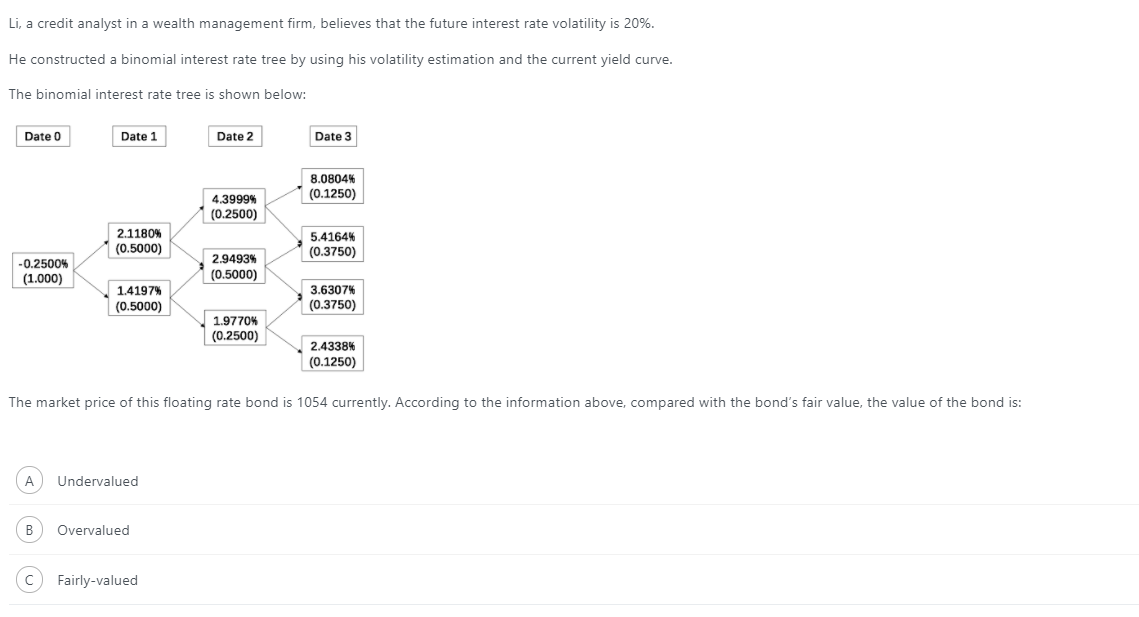
本题是要计算Floating-rate bond的Fair value；首先需要用二叉树模型计算其VND，有：
该浮动利率债券的Coupon为Benchmark rate加上4%，因此Date 4的Coupon rate出现的情况有：
8.0804%+4%；5.4164%+4%；3.6307%+4%；2.4338%+4%
因此Date 4现金流的情况：
1000×(1+0.080804+0.04)=1120.80
1000×(1+0.054164+0.04)=1094.16
1000×(1+0.036307+0.04)=1076.31
1000×(1+0.024338+0.04)=1064.34
由Date 4的现金流和二叉树所示利率，可以折现求得Date 3四个节点的Value:
1120.80/1.080804=1037.01
1094.16/1.054164=1037.94
1076.31/1.036307=1038.60
1064.34/1.024338=1039.05
由Date 2的Benchmark利率可以知道在Date 3三个节点Coupon rate出现的情况有：
4.3999%+4%；2.9493%+4%；1.9770%+4%
因此Date 3 Coupon现金流的情况：
1000×（0.043999+0.04）=84
1000×（0.029493+0.04）=69.49
1000×（0.019770+0.04）=59.77
将Date 3各个节点的Coupon加上Date 3各个节点的Value构成Date 3的总现金流，利用二叉树向Date 2折现：
[(0.5×1037.01+0.5×1037.94)+84]/1.043999=1074.21
[(0.5×1037.94+0.5×1038.60)+69.49]/1.029493=1076.03
[(0.5×1038.60+0.5×1039.05)+59.77]/1.019770=1077.30
Date 2的两个节点的Coupon由Date 1 Benchmark利率决定，因此Date 1的Coupon rate出现的情况有：
2.1180%+4%；1.4197%+4%；
因此Date 2 coupon现金流的情况：
1000×（0.021180+0.04）= 61.18
1000×（0.014197+0.04）= 54.20
Date 2的Coupon现金流加上Value现金流构成Date 2的总现金流向Date 1折现：
(1074.21×0.5+1076.03×0.5+61.18)/(1+2.1180%)=1112.73
(1076.03×0.5+1077.30×0.5+54.20)/(1+1.4197%)=1115.03
Date 1的Coupon由Date 0时刻Benchmark利率决定，因此Date 1的Coupon rate有：
-0.25%+4%
则Date 1的Coupon为：
1000×（-0.0025+0.04）= 37.50
Date 1的Coupon现金流加上Value现金流构成Date 1的总现金流向Date0折现：
(1112.73×0.5+1115.03×0.5+37.50)/(1-0.25%)=1154.27
这个1154.27为债券的VND；下面利用二叉树计算债券的CVA；
Date 4的Exposure为：
0.125×1120.80+0.375×1094.16+0.375×1076.31
+0.125×1064.34=1087.07
Date 3的Exposure为：
0.125×1037.01+0.375×1037.94+0.375×1038.60
+0.125×1039.05+0.250×84+0.5×69.49+0.250×59.77=1108.90
Date 2的Exposure为：
0.25×1074.21+0.5×1076.03+0.25×1077.30
+61.18×0.5+54.20×0.5=1133.583
Date 1的Exposure为：
1112.73×0.5+1115.03×0.5+37.50=1151.38
由以上Exposure数据，已知Recovery rate为25%，所以可以知道Recovery；再用Exposure减去Recovery可以得到Loss given default (LGD)；本题 hazard rate为1.5%，则可以算出POS以及对应POD；再用违约损失LGD乘以违约概率POD得到预期损失Expected loss；Expected loss通过折现因子求得PV(EL)；加总即得到债券的CVA；
因此由债券的VND减去其CVA可以的到Fair value：
1154.27 – 47.6019 = 1106.67；已知当前债券的市场价格为1054；则可以改债券是相对被低估的。
----------------------------------------------就算太阳没有迎着我们而来，我们正在朝着它而去，加油！
