债券

嗨，努力学习的PZer你好：

首先，2年以后债券的Macaulay duration居然没有变化。

其次，直接拿coupon再投资收益率增加的1%等同于整个债券收益率增加1%

无法理解！

------------

同学你好

这道题我重新帮你顺一下思路。

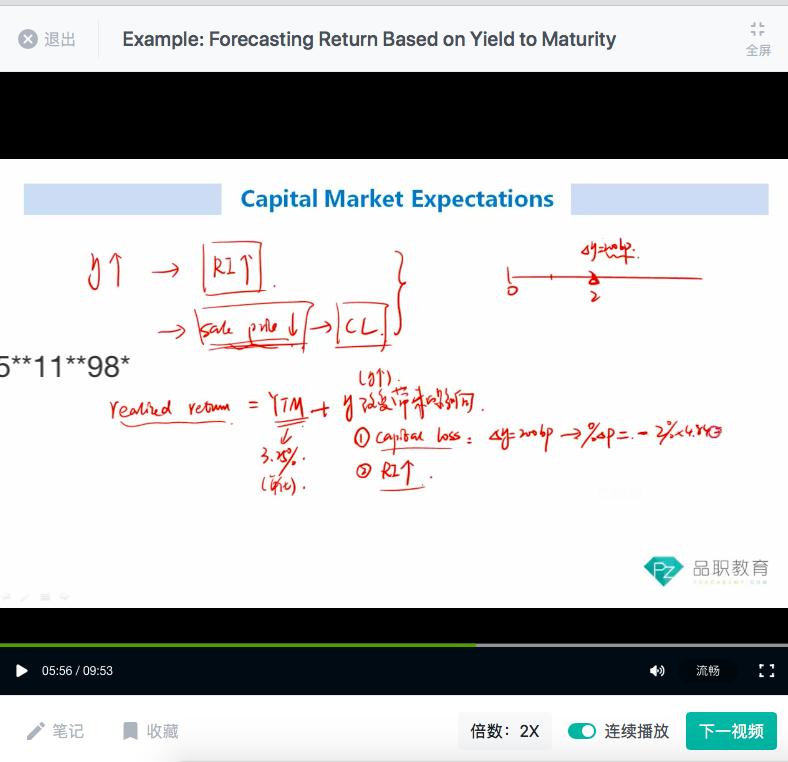
这道题考点是持有债券一段时间的expected return=YTM+收益率曲线带来的收益率变化。

如果持有期间收益率曲线未发生变化，则持有债券的收益expected return=YTM（买入时的要求回报率）；

如果收益率曲线发生变化，则会影响coupon的再投资收益产生reinvestment risk以及影响capital gain/loss产生price risk(△P/P=-△y*MD)。此时，expected return=YTM+△RI+price return①。

具体来看，如果收益率曲线上各个期限利率都提高，则△RI＞0，price return＜0；若收益率曲线上各期限利率都下降，则△RI＜0，price return＞0；同时，如果investment horizon＞macaulay duration，那么reinvestment risk影响超过price risk（比如，如果investment horizon＞macaulay duration，同时收益率曲线上各期限利率都提高，则△RI＞0，price return＜0，但|△RI|＞|price return|，此时，expected return＞YTM，也即收益率曲线上升，导致持有收益率（年化后）高于期初的YTM；如果investment horizon＜macaulay duration，同时收益率曲线上各期限利率都提高，则△RI＞0，price return＜0，但|△RI|＜|price return|，此时，expected return＜YTM，也即收益率曲线上升，导致持有收益率（年化后）低于期初的YTM；如果investment horizon=macaulay duration，同时收益率曲线上各期限利率都提高，则△RI＞0，price return＜0，但|△RI|=|price return|，此时，expected return=YTM，即持有期间收益率曲线变动对持有收益率（年化）没有太多影响，持有收益率（年化）基本等于买入时的YTM）

在上面理论的基础上，我们来看这道题。

题目首先计算macaulay duration，根据modified duration=macaulay duration/(1+ytm)这个公式，我们可以计算出期初买入时，portfolio的macaulay duration=4.84*1.0325=5.0，那么，如果投资期限是5年，macaulay duration=investment horizon，price risk与reinvestment risk可以相互抵消，收益率曲线变动对持有期收益率几乎没有影响，expected return年化后=YTM。

然后根据题目已知条件，未来两年，收益率曲线将上升2%。分别让计算持有2年、5年、7年的预期收益率。

首先，期初已知MD=4.84，持有期△y=2%，△P/P=-MD*△y=-9.68%，只要投资2年及以上（因为利率用了两年提高2%），price return都是-9.68%（非年化）。

我们以2年、5年为例计算△RI。

投资2年时：

本题假设利率平缓上涨，每年增长1%。那么，第一次利率上涨是发生在第一年末，影响第第二年的再投资收益，所以第一年末收到coupon在第二年的再投资收益上涨了1%；第二次利率上涨发生在第二年末，影响收到coupon在第三年及以后年份的再投资收益。

由于投资期只有两年，因此，只有第一年末的coupon在第二年的再投资收益增加1%，不存在第三年及以后年份的再投资收益。

所以，如果投资两年，总的△RI=1%，price return=-9.68%，所以根据公式①expected return=3.25%-9.68%/2+1%/2=-1.09%，相当于年化的expected return为-1.09%。

投资5年时：

投资5年的price return不变，仍为-9.68%。

而coupon的再投资收益发生变化，因为从第二年末，第三年初开始，再投资收益增加2%，影响第三年、第四年、第五年的coupon再投资收益。所以，coupon的再投资收益增加额为1%（第二年期间）+2%（第三年期间）+2%（第四年期间）+2%（第五年期间）=7%，

所以，如果投资5年，总的△RI=7%，price return=-9.68%，根据公式①expected return=3.25%-9.68%/5+7%/5=2.714%。

以此类推。

这道题的思考方式比较新颖，同学自己慢慢琢磨一下这个过程。

----------------------------------------------
努力的时光都是限量版，加油！