三级押题3-第25题 - Macaulay Duration

嗨，努力学习的PZer你好：

请问答案中12.0008 是怎么算出来的

这个不是3级的考纲要求，应该在1级有考纲要求（可能一级从来就没有考过），在3级一般会直接给我们这个Macaulay duration数据的。下面就大概说一下这个12.0008是如何算到的，最终需要知道按照定义计算的Macaulay duration会更加准确，而用简单的加权平均算Portfolio macaulay duration会有误差。12.0008就是严格按照Macaulay duration的定义计算的：

第一步：根据表格里的3支债券的情况，我们可以写出这个Portfolio在每一期的现金流。

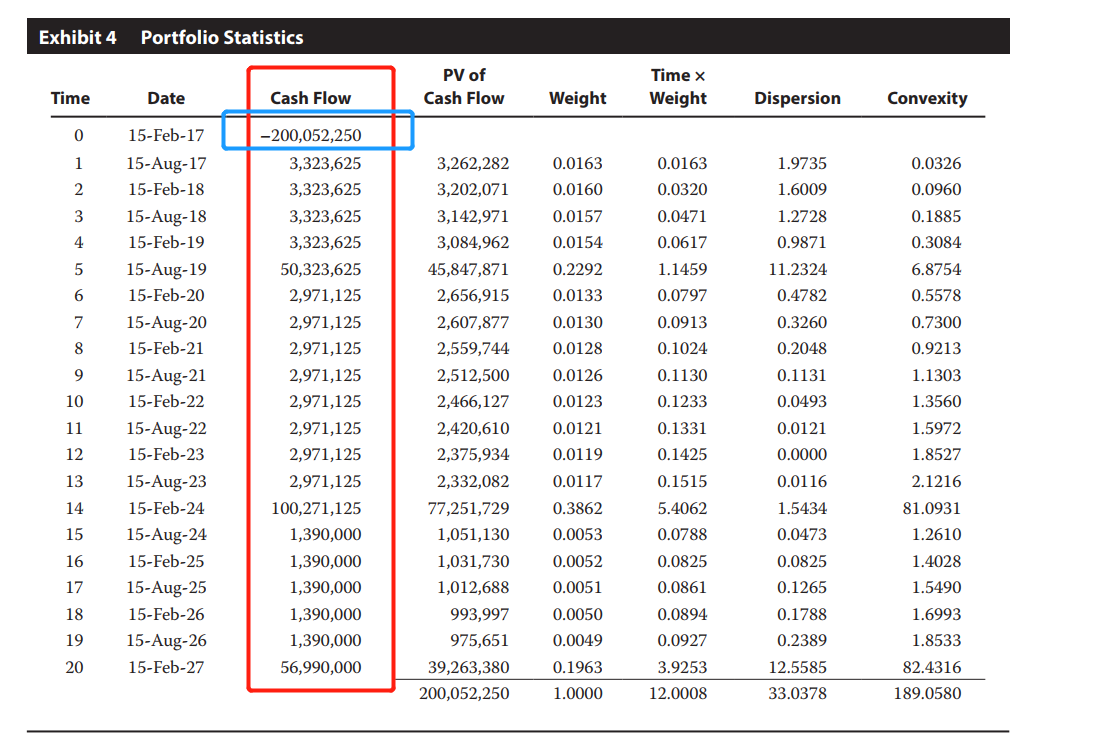
如下图第三列红框的Cash flow，我们期初买入Portfolio需要花费200,052,250，代表现金流的流出；然后后面逐期我们会拿到组合内各个债券的现金流，如，在17年Aug.15，会拿到3支债券的Coupon：

第一支债券的Coupon是：47000000×1.50%/2 = 352,500

第二只债券的Coupon是：97300000 × 3.25%/2 = 1,581,125

第三支债券的Coupon是：55600000 × 5% /2 = 1,390,000

加总之后，就是17年AUG.15的总现金流：3,323,625

同理，其他每一期的现金流都可以算出来。每一期的现金流就是3支债券的现金流加总。

有了这个Portfolio的现金流分布，我们就可以把它当成债券，算出Portfolio的内部收益率Cash flow yield，他相当于是Portfolio的Yield-to-maturity；

第二步：对每一期的Cash flow用Cash flow yield进行折现，就会得到第4列的PV Of cash flow，这是算出每一期Cash flow的现值。

第三步：有了每一期现金流的现值，我们就可以算出来第5列的现金流的权重Weight，他是本期的现金流现值除以现金流现值总和。

第四步：用每一期现金流的权重，乘以该笔现金流的发生时间，我们就可以算出来第六列的Time × Weight；

把第六列的Time × weight加总之后，就是12.0008。

12.0008代表的是债券现金流发生的平均时间，因为我们是对现金流发生时间做了加权平均，而时间的权重是各期现金流现值的占比。这其实就是Macaulay duration的概念，是债券现金流发生时间的加权平均。

只不过在本题里，这个债券是半年付息一次，所以12.0008还要再除以2，就是年化后的Macaulay duration，就是6了。代表的意思是，我们投资这支债券，平均来看，收到所有的现金流需要花费6年。

以上是Macaulay duration按照定义的计算方法，不是3级需要掌握的内容。

----------------------------------------------
虽然现在很辛苦，但努力过的感觉真的很好，加油！