这题是pzqa015回答我无法理解,辅导员老师让我重新问一遍其他老师。此外,我发现漏回答的两题也是pzqa015回答期间漏掉的,不是其他老师的责任,在此澄清。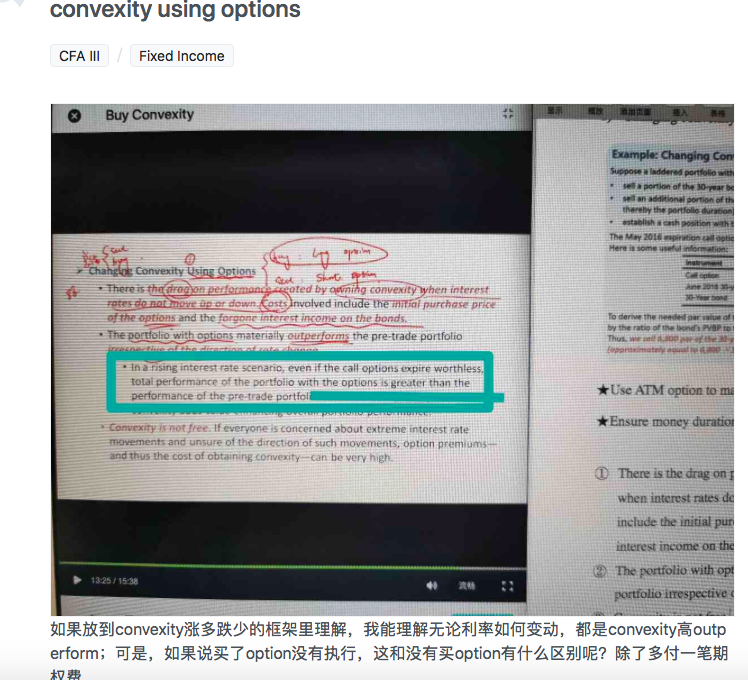

发亮_品职助教 · 2021年05月27日
嗨,爱思考的PZer你好:
那他可能还是亏的吧?option很贵,涨多跌少跌再少也不够期权费吧⊙﹏⊙
不一定,具体要看利率的波动幅度。
就是因为期权费很贵,所以我们说Buy convexity策略是一个会付出成本的策略,所以我们要求,利率的改变最好能尽快发生,这样我们Increase convexity付出的持有成本就少。
如果利率迟迟都没有改变,我们为了Increase convexity会一直持有Option,这样其实是一直在付出Option的时间价值。
同时,利率的变动幅度还不能太小,太小的话,可能Convexity涨多跌少的收益还比不上期权费贵。
我们原版书这道题,就是他买入了即将到期的Option,因为是即将到期,Option几乎没有多少时间价值了,于是Option比较便宜,共买入了9640 par value的Option,Market value是:383,000;
同时,卖出的30-year bond的Convexity是5.959,而买入Option的Convexity是826.041,因此这么操作之后极大地提高了Portfolio的Convexity。通过合适的配比,让Portfolio的Duration没有改变。
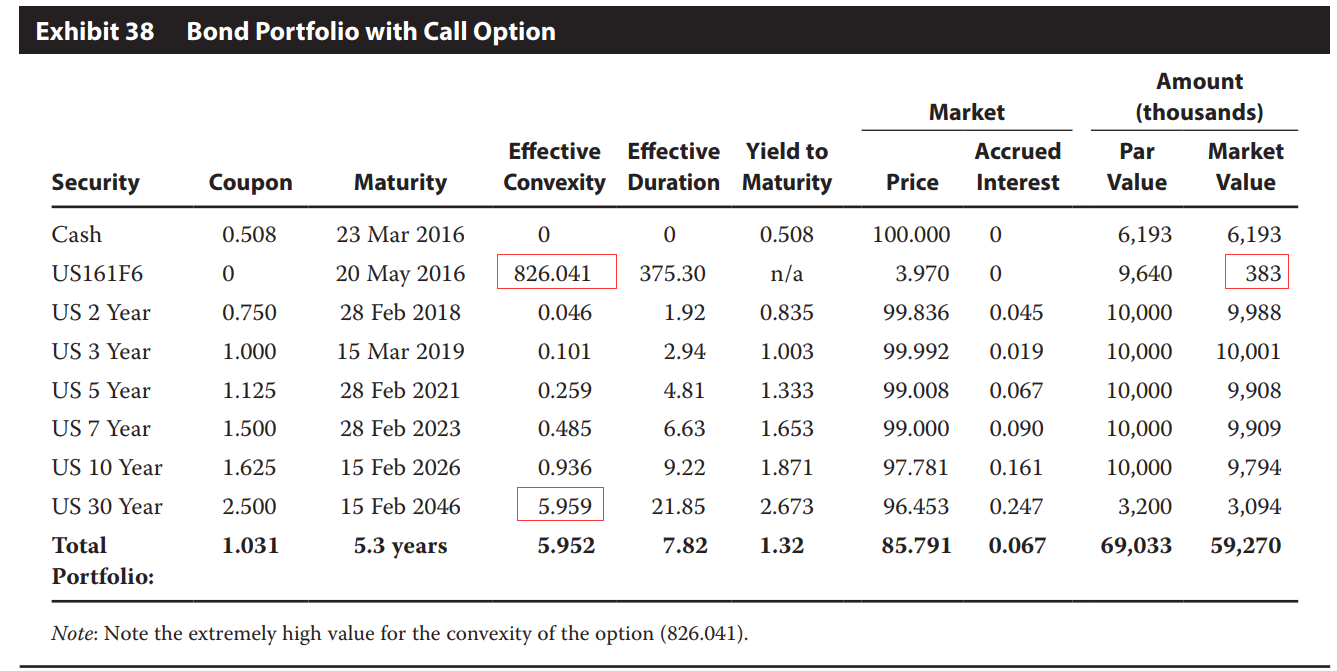
然后原版书替我们算了一下该策略的收益。Post-trade portfolio是指使用了Option之后的Portfolio;而Pre-trade portfolio是指调整策略之前的Portfolio。
从表格里的数据也可以看到,当利率上升只有+25bps时,买入Options increase convexity其实是亏损的策略。这就是涨多跌少比不上Increase convexity付出的成本。
所以我们说,当预期利率的波动比较小的时候,通过Buy options来Increase convexity的策略有可能是亏损的策略。
发现只有当利率上升的幅度大于+50bps时,Buy options increase convexity的策略才会有收益。
从课后题和Mock题可以判断,这种题型多是定性的题目,也就是说,基本上都是Yield curve volatility上升,我们可以选择合适的策略是Buy convexity的策略。考试的话估计基本是这种定性。定量的话涉及到的计算稍微有些麻烦,估计不太会出题。
----------------------------------------------
努力的时光都是限量版,加油!
发亮_品职助教 · 2021年05月25日
嗨,从没放弃的小努力你好:
那这里讲的只是in a rising interest rate scenario,而不是a rising volatility scenario,为什么能赚取期权费价差呢?
我翻看了下原版书,这段In a rising interest rate scenario是承接着后面这道例题的。

大背景是:他先卖出了Portfolio里面的30-year bond,然后买入了Options,同时因为Option本身就有Duration,所以合适的配比就保证了这样的买卖前后组合的Duration没有改变。但是因为Options有极大的Convexity,这么操作之后,组合的Convexity变大了。
首先就是在Interest rate volatility加大时,Buy option可以获利,第一个回复已经解释过了。
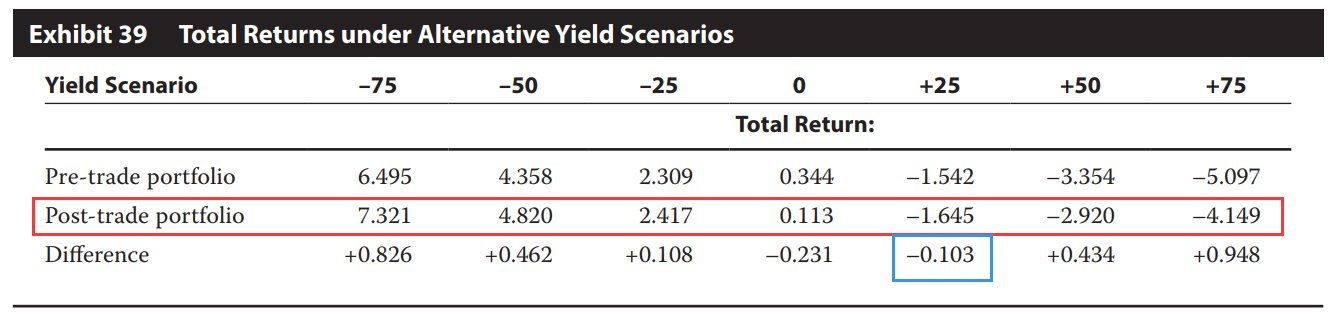
那现在接下来原版书在讨论,如果当利率上升时,Buy option这个策略如何影响收益。首先就是当利率上升时,组合其实是有损失的,因为利率上升通过Duration会对组合产生Capital loss,但因为买卖Option前后组合的Duration一致,因此从这点上来说Buy option对组合没有影响。
但是由于Buy options之后组合拥有很大的Convexity,无论利率涨跌,Convexity对债券的影响都是正向的,因此,Buy options之后组合的Capital loss会相对较小一些。于是原版书这里就说,就算利率是上升的,Option没有被行权,有Option的组合也比之前的组合表现更好。如下图:

----------------------------------------------
加油吧,让我们一起遇见更好的自己!
发亮_品职助教 · 2021年05月23日
嗨,努力学习的PZer你好:
其实不用考虑Option的执行问题。
因为在2级学过,Option的价格是Volatility的函数,只要Volatility升高,Option的价格一定会上升。
那这样的话,期初我们买入Option时,是以较低Volatility定价出来的Option Premium买入,由于我们预期未来Volatility会上升,那意味着我们预期未来的Option价格一定会上升,那此时,在未来时刻我们以更高的价格卖出Option即可。买卖价差就是Volatility上升时,Option的“Convexity”带来的额外收益。
这样的话就已经赚取了Volatilty升高的收益了,无需考虑Option的行权问题。
----------------------------------------------
加油吧,让我们一起遇见更好的自己!