NO.PZ2019103001000055
问题如下:
Abram’s supervisor disagrees with Abram’s yield curve outlook. The supervisor develops two alternative portfolio scenarios based on her own yield curve outlook:
Scenario 1:Sell all bonds in the Fund except the 2-year and 30-year bonds, and increase positions in these two bonds while keeping duration neutral to the benchmark.
Scenario 2:Construct a condor to benefit from less curvature in the 5-year to 10-year area of the yield curve. The condor will utilize the same 1-year, 5-year, 10-year, and 30-year bonds held in the Fund. The maximum allowable position in the 30-year bond in the condor is $17 million, and the bonds must have equal (absolute value) money duration.
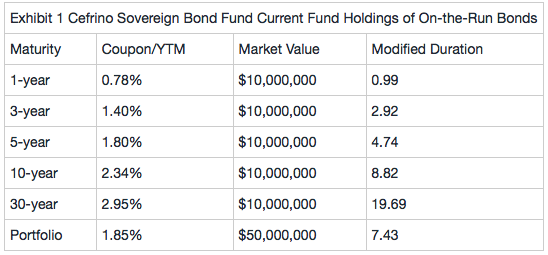
Based on Exhibit 1, which short position is most likely to be included in the condor outlined in Scenario 2?
选项:
A. 1-year $338 million
B. 5-year $71 million
C. 10-year $38 million
解释:
A is correct.
To profit from a decrease in yield curve curvature, the correct condor structure will be: short 1s, long 5s, long 10s, and short 30s. The positions of the condor will be: short $338 million 1-year bond, long $71 million 5-year bond, long $38 million 10-year bond, and short $17 million 30-year bond.
This condor is structured so that it benefits from a decline in curvature, where the middle of the yield curve decreases in yield relative to the short and long ends of the yield curve.
To determine the positions, we take the maximum allowance of 30-year bonds of $17 million and determine money duration. Money duration is equal to market value x modified duration divided by 100. 30-year bond money duration = $17 million × 19.69/100 = $3,347,300. The market values of the other positions are:
1-year bond: $3,347,300 × 100/0.99 = $338.11 million or $338 million
5-year bond: $3,347,300 × 100/4.74 = $70.62 million or $71 million
10-year bond: $3,347,300 × 100/8.82 = $37.95 million or $38 million
为啥market duration还要除以100呢?



