问题如下:
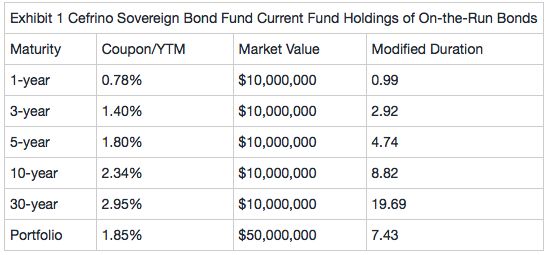
Edgarton evaluates the Fund’s positions from Exhibit 1 along with two of his pro forma portfolios, which are summarized in Exhibit 2:
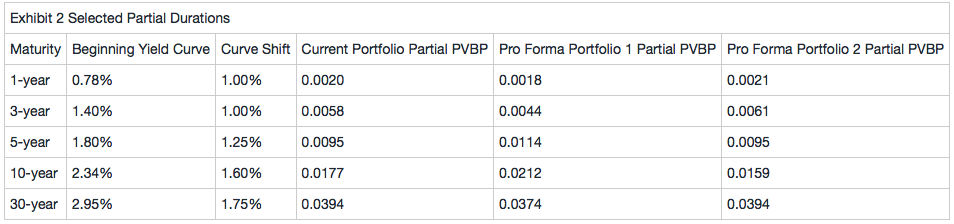
Edgarton expects a steepening yield curve, with short-term yields rising by 1.00% and long-term yields rising by more than 1.00%.
Based on Exhibits 1 and 2, which of the following portfolios is most likely to have the best performance given Edgarton’s yield curve expectations?
选项:
A. Current Portfolio
B. Pro Forma Portfolio 1
C. Pro Forma Portfolio 2
解释:
C is correct.
Given Edgarton’s expectation for a steepening yield curve, the best strategy is to shorten the portfolio duration by more heavily weighting shorter maturities. Pro Forma Portfolio 2 shows greater partial duration in the 1- and 3-year maturities relative to the current portfolio and the least combined exposure in the 10- and 30-year maturities of the three portfolios. The predicted change is calculated as follows:
Predicted change = Portfolio par amount × partial PVBP × (-curve shift in bps)/100
我看到Carolllll在几个月前的一个问题回复,还是有疑问。各期限market value是等权重的啊,哪里看出1年和3年的持有比例高了?我倒觉得在同等权重的情况下portfolio 1的30年PVBP最小,30年期Dration一定的情况下,受利率上浮变化的影响也最小(也就是在利率上升的时候亏损最小),所以应该选B,我这思路错哪了,请指点,谢谢。


