问题如下:
Exhibit 1 shows par, spot, and one-year forward rates.
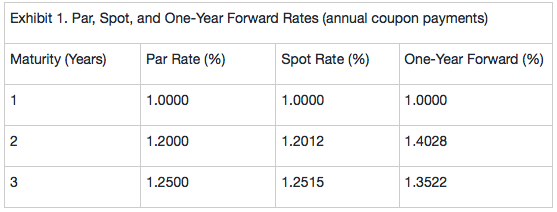
Bond 4 is a fixed-Rate Bonds of Alpha Corporation, with 1.55% annual coupon and callable at par without any lockout periods. The bond maturity is 3 years.
Based on the information above, the value of the embedded option in Bond 4 is closest to:
选项:
A.nil.
B.0.1906.
C.0.3343.
解释:
C is correct.
考点:考察对含权债券的理解
解析:
债券4是可Callable。其价值为:
Value of callable bond = value of straight bond – value of call option on bond
因此,Embedded call option的价值为:
Value of call option on bond = Value of straight bond – Value of callable bond
利用Spot rate对该Straight bond进行定价为:
而Callable bond的定价需要使用1-year forward rate,将债券的现金流从最后一期开始,依次向前一个节点折现,以判断折现值是否会触发行权价;使用表格中的Forward rate对Callable bond进行定价:
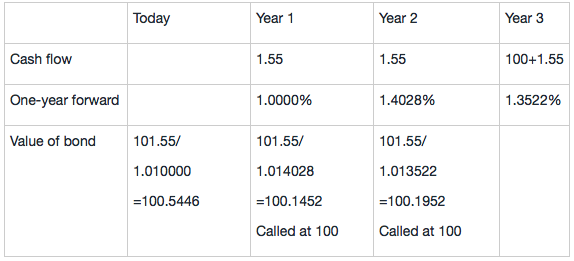
因此Call option的Value为:100.8789-100.5446=0.3343
请问embedded option value为何可以直接用forward rate求?不应该是用forward rate(middle rate)用公式求出HH和HL,然后再用二叉树从后往前推算吗?请问这个知识点在哪里?谢谢



