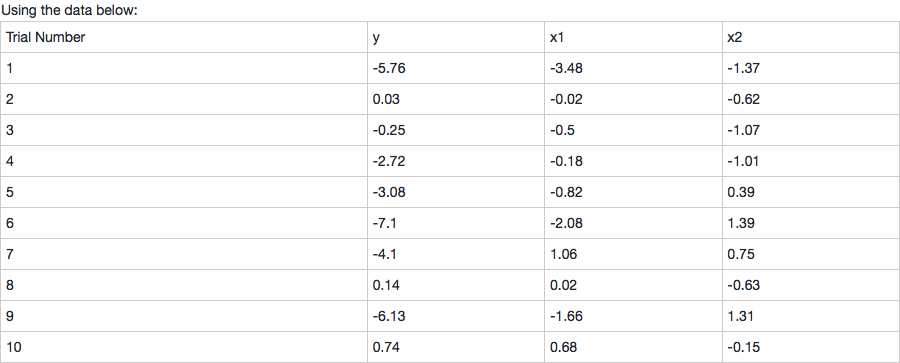
问题如下:
a. Apply OLS linear regression to find the parameters for the following equation:
Yi=α+β1X1i+β2X2i+ϵi
选项:
解释:
Start by setting up the basic calculations:




μY=−2.823,μX1=−0.91,μX2=−0.101,
σY2=7.58,σX12=1.345,σX22=0.911
σX1X2=−0.172,σYσX1=2.729,σYσX2=−1.434
First regressing on the last independent variable:
X1i=δ0+δ1X2i+X1i
δ1=σX22σX1X2=−0.172/0.911=0.189
δ0=μX1−δ1μX2=−0.91−0.189∗(−0.101)=−0.929
Yi=γ0+γ1X2i+Yi
γ1=σYX2/σX22=−1.434/0.911=−1.574
γ0=μY−γ1μX2=−2.823−(−1.574∗−0.101)=−2.982

so β1=σX12Cov()Y,X1=2.459/1.313=1.873
Repeating the process for X2
β2=−1.085/0.889=−1.221
Tying things together:
Yi−β1X1i−β2X2i=α+ϵi=−1.873X1i+1.221X2i

So α=−1.242, and the variance of the residuals is 0.718.
Finally, asserting the presumption of normality:
Yi=−1.242+1.873∗X1i−1.221∗X2i+ϵi,ϵi N(0,0.718)
Note that the variance for ϵi is biased and the unbiased figure is this figure multiplied by 10/(10 - 3) or 1.206.