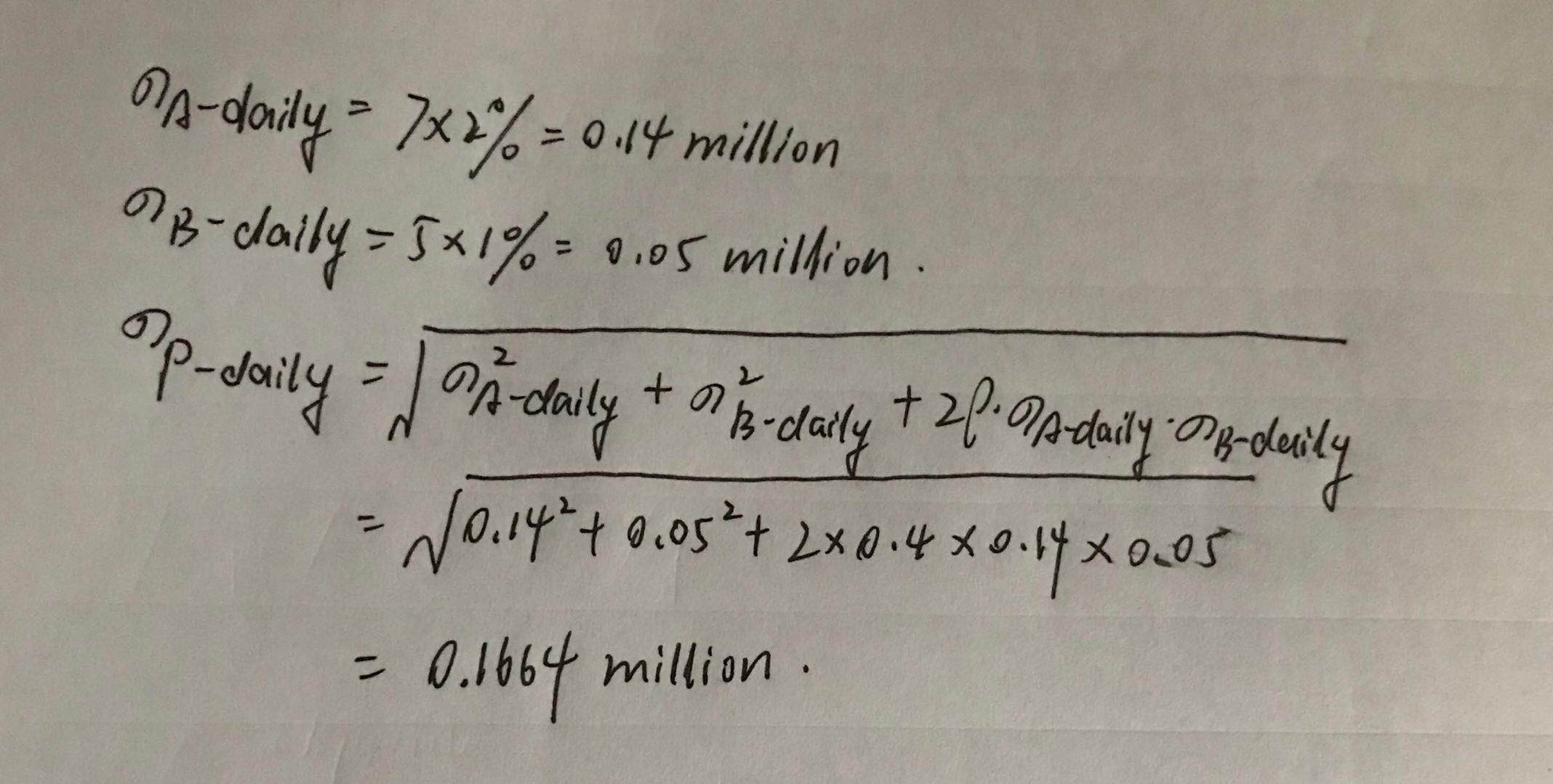问题如下:
Suppose a financial institution has a two-asset portfolio with $7 million in asset A and $5 million in asset B. The portfolio correlation is 0.4, and the daily standard deviation of returns for asset A and B are 2 % and 1 % , respectively. -what is the 10- day value at risk (VaR) of this portfolio at a 99% confidence level ( α = 2.33)? Supposed the mean of portfolio returns is zero.
选项:
A.
$1.226 million.
B.
$1.670 million.
C.
$2.810 million.
D.
$3.243 million.
解释:
A
The first step in solving for the 10-day VaR requires calculating the covariance matrix.
l c o v 11 = σ 1 2 = 0.0 2 2 = 0.0004 c o v 22 = σ 2 2 = 0.0 1 2 = 0.0001 c o v 12 = ρ 1 , 2 × σ 1 × σ 2 = 0.4 × 0.0 2 × 0.01 = 0.00008 {l}{\mathrm{cov}}_{11}=\sigma_1^2=0.02^2=0.0004\\{\mathrm{cov}}_{22}=\sigma_2^2=0.01^2=0.0001\\{\mathrm{cov}}_{12}=\rho_{1,2\times}\sigma_1^{}\times\sigma_2=0.4\times0.02^{}\times0.01=0.00008 l c o v 1 1 = σ 1 2 = 0 . 0 2 2 = 0 . 0 0 0 4 c o v 2 2 = σ 2 2 = 0 . 0 1 2 = 0 . 0 0 0 1 c o v 1 2 = ρ 1 , 2 × σ 1 × σ 2 = 0 . 4 × 0 . 0 2 × 0 . 0 1 = 0 . 0 0 0 0 8
Thus, the covariance matrix C, can be represented as:
( 0.0004 a m p ; 0.00008 0.00008 a m p ; 0.0001 ) (\begin{array}{cc}0.0004&0.00008\\0.00008&0.0001\end{array}) ( 0 . 0 0 0 4 0 . 0 0 0 0 8 a m p ; 0 . 0 0 0 0 8 a m p ; 0 . 0 0 0 1 )
Next, the standard deviation of the portfolio, σ p \sigma_p σ p
Step 1: Compute β h \beta_h β h × C:
l [ 7 , 5 ] ( 0.0004 a m p ; 0.00008 0.00008 a m p ; 0.0001 ) = [ ( 7 × 0.0004 ) + ( 5 × 0.00008 ) a m p ; ( 7 × 0.00008 ) + ( 5 × 0.0001 ) ] = [ 0.0032 a m p ; 0.00106 ] {l}{\lbrack7,5\rbrack}{(\begin{array}{cc}0.0004&0.00008\\0.00008&0.0001\end{array})}\\={\lbrack{(7\times0.0004)}+{(5\times0.00008)}\begin{array}{cc}&\end{array}{{(7\times0.00008)}+{(5\times0.0001)}\rbrack}}\\={\lbrack0.0032\begin{array}{cc}&\end{array}}{0.00106\rbrack} l [ 7 , 5 ] ( 0 . 0 0 0 4 0 . 0 0 0 0 8 a m p ; 0 . 0 0 0 0 8 a m p ; 0 . 0 0 0 1 ) = [ ( 7 × 0 . 0 0 0 4 ) + ( 5 × 0 . 0 0 0 0 8 ) a m p ; ( 7 × 0 . 0 0 0 0 8 ) + ( 5 × 0 . 0 0 0 1 ) ] = [ 0 . 0 0 3 2 a m p ; 0 . 0 0 1 0 6 ]
Step 2: Compute ( β h \beta_h β h × C)* β v \beta_v β v
l [ 0.0032 a m p ; 0.00106 ] [ 7 5 ] = ( 0.0032 × 7 ) + ( 0.00106 × 5 ) = 0.0277 {l}{\lbrack0.0032\begin{array}{cc}&\end{array}}{0.00106\rbrack}{\lbrack\begin{array}{c}7\\5\end{array}\rbrack}\\={(0.0032\times7)}+{(0.00106\times5)}=0.0277 l [ 0 . 0 0 3 2 a m p ; 0 . 0 0 1 0 6 ] [ 7 5 ] = ( 0 . 0 0 3 2 × 7 ) + ( 0 . 0 0 1 0 6 × 5 ) = 0 . 0 2 7 7
Step 3:Compute σ p \sigma_p σ p
σ p = β h × C × β V = 0.0277 = 0.1664 \sigma_p=\sqrt{\beta_h\times C\times\beta_V}=\sqrt{0.0277}=0.1664 σ p = β h × C × β V = 0 . 0 2 7 7 = 0 . 1 6 6 4
The 10-day portfolio VaR(in millions) at the 99% confidence level is then computed as:
V a R P = σ P α X = 0.1664 × 2.33 × 10 = VaR_P=\sigma_P\alpha\sqrt X=0.1664\times2.33\times\sqrt{10}= V a R P = σ P α X = 0 . 1 6 6 4 × 2 . 3 3 × 1 0 =
老师,请问这个解析讲义上有类似例题么?我听完了市场风险部分,但是对解析过程没有印象啊…