问题如下:
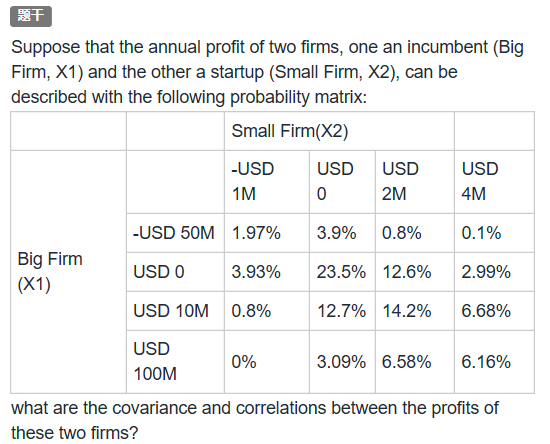
Suppose that the annual profit of two firms, one an incumbent (Big Firm, X1) and the other a startup (Small Firm, X2), can be described with the following probability matrix:

what are the covariance and correlations between the profits of these two firms?
选项:
解释:
First, the two means and variances can be computed from the marginal distributions.
Then the covariance can be computed using the alternative form, which is .
The means can be computed using for j = 1,2.
The variance can be computed using , which requires computing using .
For Big Firm, these values are , and .
For Small Firm, these values are , and .
The expected value of the cross product is . The covariance is then 43.22 - 1.25 * 15.88 = 23.37 and the correlation is
没有图