LizLiu · 2020年01月08日
* 问题详情，请 查看题干
问题如下：
Based on Exhibit 3, the implied Australian dollar (A$) 1-year rate, 1-year forward is closest to:
选项：
A.0.15%.
B.1.95%.
C.2.10%.
解释：
B is correct.
The implied forward rate can be calculated using the yield to maturity (YTM) of the 2-year Ride-the-Yield Curve and 1-year Buy-and-Hold portfolios.
F1.1=[(1.018)2/1.0165]-1=1.95%
riding the yield curve的portfolio, 一年以后的价格是100.1，为什么不是用到期的时候101.75除以100.1再减一得到forward(1,1)呢，这个折现时候用的利率，不就是预计的1年以后1年期的利息吗。。。
发亮_品职助教 · 2020年01月09日
嗨，努力学习的PZer你好：
“riding the yield curve的portfolio, 一年以后的价格是100.1，为什么不是用到期的时候101.75除以100.1再减一得到forward(1,1)呢”
Implied forward rate按照定义就是用两个Spot rate卡出来的。
例如，2年期的Spot rate、与1年期的Spot rate，可以算出来一个f(1,1)，也就是站在现在时刻看，第1年年末开始、未来1年的利率。
因为当前时刻的长期利率，可以看成是先以当前的短期利率借贷、到期后以未来的利率再滚动一笔借贷、实现长期，所以有由一个长期、一个短期利率算出来的这个Forward rate就是站在现在时刻看，未来滚动借贷时的借贷利率。
这个Forward rate是隐含在当前时刻长、短期利率差异之间的。
本题因为预测的是Stable yield curve，未来的到期价100.1等等，其实是假设未来利率不变、也就是和当前利率一致算出来的价格。
预测未来利率和现在一样，就说明将来时刻，没有实现当前隐含的Forward rate；
这个价格是假设Stable yield curve算出来的，和当前Spot rate里隐含的、发生在未来时刻的利率无关。
所以，如果要算Forward rate，就需要用两个Spot rate计算。
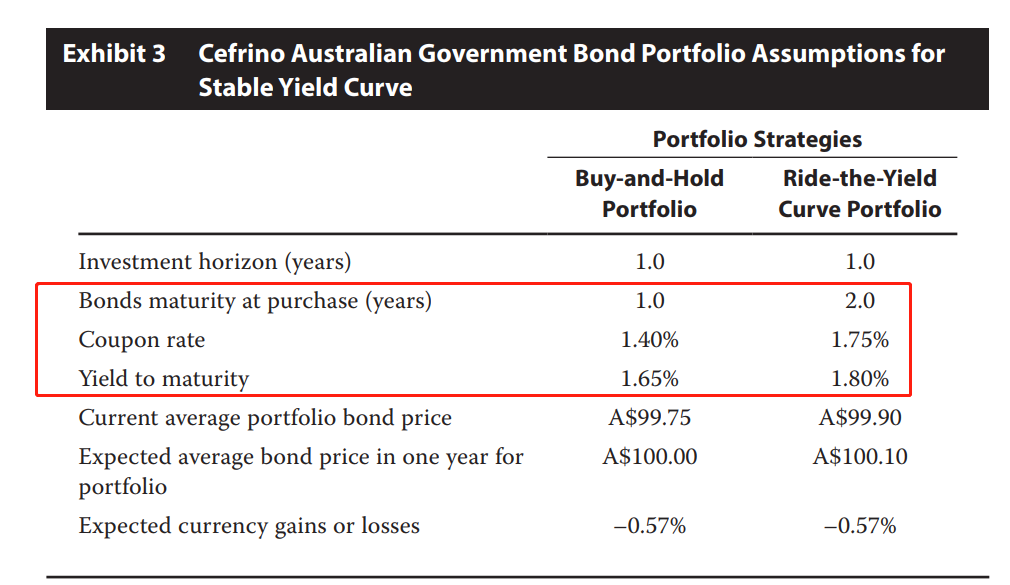
这道题的表格只需要看这部分就行：
2年期债券持有至到期的利率是1.80%
1年期债券持有至到期的利率是1.65%
理论上，我们应该先用付息债券持有至到期收益率YTM，算出来零息国债的Spot rate，再由Spot rate算Implied forward rate；
但这道题数据差异很小，就把2年期付息国债的YTM当成了2-year spot rate；1年期付息国债的YTM当成了1-year spot rate，两个YTM可以直接算Implied forward rate。
Implied forward rate需要按照两个Spot rate计算即可。原版书的这道题是乱入三级，我们三级实际上不涉及这知识点。
-------------------------------加油吧，让我们一起遇见更好的自己！
徐威廉 · 2021年10月19日
发亮大神老师，关于S1等于YTM1这个1.65%不对啊，这个是付息债啊，怎么求spot rate呢？ 还有S2更不知道为啥会等于1.8%
NO.PZ201812020100000808 1.95%. 2.10%. B is correct. The implieforwarrate ccalculateusing the yielto maturity (YTM) of the 2-yeRi-the-YielCurve an1-yeBuy-anHolportfolios. F1.1=[(1.018)2/1.0165]-1=1.95%s1和s2到底是根据buy anhol据求还是ri the yielcurve求？
NO.PZ201812020100000808 前面有解答提到 “ring the yielcurve的E(R)正常就应该等于implieforwarrate”这个结论只适用于零息债券 我不太理解老师们的这个解答是什么意思。按照我的计算，即便是付息债券，2年期债券ring the yielcurve，在1年期卖掉时的价格为 1.75+(1.75+100)/(1+1.65%)=101.8483 那么ring the yielcurve的一年期持有收益率就是101.8483/99.9 - 1 = 19.5%，与直接用YTM们计算出来的implieforwarrate完全相同，是适用的。 唯一的问题是，表格中对于2年期的债券，凭什么预期认为1年期的卖价也是100？这个数字很是奇怪。
NO.PZ201812020100000808 我记得课上老师讲过ring the yielcurve的E(R)正常就应该等于implieforwarrate，但是这道题，经过计算ring the yielcurve后的E(R)等于1.28%，就算不考虑currenloss那也是1.85%不等于答案中的1.95%，请问这是怎么回事？
1.018是什么？为什么上面还要算一遍1.08?
