2*mid-term yield -short term yield - long term yield
如果中期利率下降,两边上升,这个数字也有可能是负的,讲义是说larger butterfly spread等于more curvature,这种情况下,是不是不对啊,应该是绝对值larger。
发亮_品职助教 · 2020年01月07日
嗨,从没放弃的小努力你好:
"如果短期3%,中期2%,长期3.5%, butterfly spread=-2.5%, 中期利率上升,短期长期不变,变成中期3%, butterfly spread=-0.5%, 这个数字变大了,但是线变得没那么弯了。。。这样的变化也是more curvature?"
从数字上看,收益率曲线是More curvature,但从实际图形上看是Less curvature。
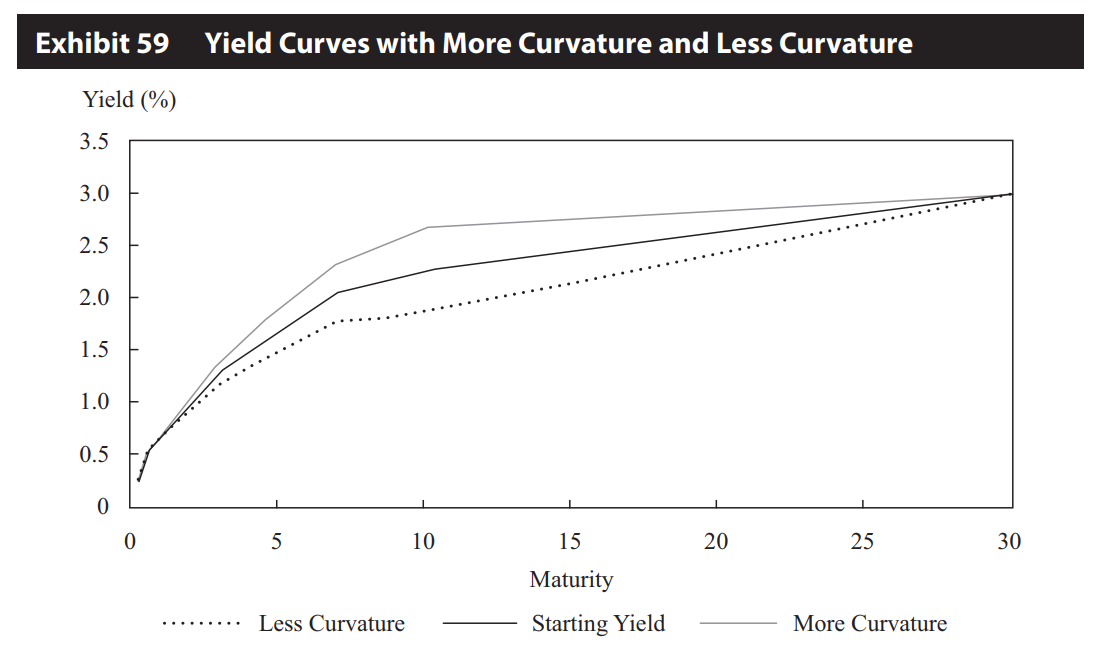
出现这样的是因为咱们的分析框架是在Normal curve下。也是最常见的短期、中期、长期关系图,如下面截图:
如截图里的这种情况,就是会使得2倍的中期利率减去短期、长期利率为一个正数。所以Butterfly spread越大代表More curvature。
如果是提问这种情况的话,再用Normal curve这种情形来分析,那刚好判断就是反的。不过因为像提问里的利率情况基本很难存在,所以分析框架就只记住Normal下的即可。因为原版书也只给了默认是正Spread的情况,所以记住Normal情况应对考试是没有问题的。
或者,如果想把不常见的情况包含进来,记绝对值也行,Butterfly spread反正就是描述中期利率,相对长、短利率的位置,那直接记绝对值也行,绝对值越大,说明中期和长、短期的相对位置越远,代表弯曲程度越大。
“同理也想问steepening, 如果收益率曲线原来就是短期比长期利率高,invert的这种,那么,如果短期涨得更高,数字上spread是变得更小了,那么这是steepening还是flattening”
衡量陡峭程度的是:Yield Curve Spread = 长期利率 - 短期利率;Spread越大,代表曲线越陡峭。这个也只针对Normal curve。
如果这个Spread减下来是负数,我们可以判断收益率曲线是Inverted的。
但是,如果收益率曲线已经是Inverted yield,然后还想用Yield curve spread来判断是Flattening/还是Steepening,如果按Normal的情况分析刚好是反的。所以建议只用记Normal状况下,Spread越大,代表曲线越陡峭。查了原版书这点是没问题的。
或者反正陡峭程度衡量的是短期利率相对长期利率的位置,那记一个绝对值也行,绝对值越大说明长、短期的相对位置越远,越陡峭。绝对值越小,代表长短期利率的相对位置越近,越平坦。
原版书给的也是正常情况,所以默认两个Spread减下来都是正数,数据越大代表越弯曲/陡峭。
提问里的这种情况我开始也没想到,所以按Normal的思路分析Inverted情况刚好是反的。如果记绝对值就完全不会存在这种冲突,所以觉得方便记绝对值也OK。绝对值越大代表中期与长短期的差异越大,越弯曲。
-------------------------------
加油吧,让我们一起遇见更好的自己!
发亮_品职助教 · 2020年01月06日
嗨,从没放弃的小努力你好:
不用加绝对值。
2*mid-term yield -short term yield - long term yield,反应的就是中期利率相对于短期、长期利率的位置。
是一个静态量,减出来的数字越大代表此刻收益率曲线越Curvature,越小代表越Less Curvature
如果说是中期下降、长短期上升,变动后收益率曲线有更低的Mid-term,更高的Short-term/Long-term的利率,那减出来的值会变小。
所以对于Butterfly spread,由变动前一个更大的值,变成了此刻一个更小的值,数值变小,所以知道收益率曲线是Less curvature。
和讲义里说的Larger butterfly spread代表More curvature是一致的。
Butterfly spread这是一个静态数字,就是反应此刻收益率曲线的弯曲程度。如果要比较收益曲线弯曲程度的变化,就需要用变动前后两个Butterfly spread来比较了。
如果要衡量动态数字,就是收益率曲线变动前后Curvature的变化量,那就带入利率的变动值数据:
2 × Δmid-term yield - Δshort term yield - Δlong term yield
他就可以衡量Butterfly spread的变量,是一个动态数据。
如果是中期利率下降,长期、短期利率上升,那代表 Δmid-term yield是负数, Δshort term yield、Δlong term yield为正数,那减下来的数值是负数,我们可以知道这个变动会给收益率曲线带来负的ΔButterfly spread变化,所以收益率曲线是变得更Less curvature的。
但是这个数值减下来只能反映收益率曲线前后的变化程度,并不能反映此刻收益率曲线的弯曲程度。
如果要知道此刻的弯曲程度,就需要拿变动后、新的利率求一个Butterfly spread = 2*mid-term yield -short term yield - long term yield
-------------------------------
虽然现在很辛苦,但努力过的感觉真的很好,加油!
LizLiu · 2020年01月07日
同理也想问steepening, 如果收益率曲线原来就是短期比长期利率高,invert的这种,那么,如果短期涨得更高,数字上spread是变得更小了,那么这是steepening还是flattening