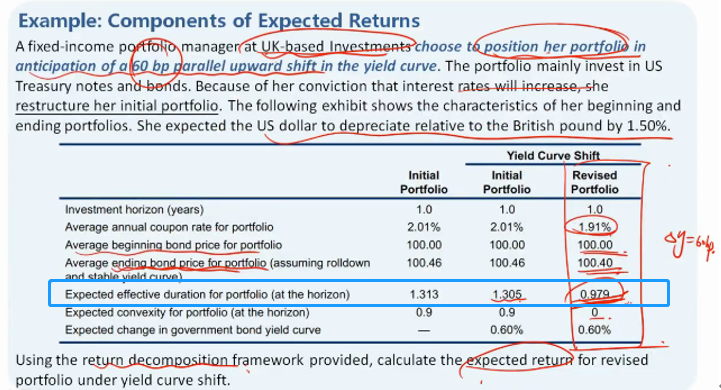
请教老师圈出的这一行的每一个duration的意思,为何有不同。三者有什么关系?
我理解第一个1.313是开始的duration,最后一个0.979是修改后的duration,此处核心是对中间哪一些不太明白。
发亮_品职助教 · 2019年12月29日
“对于第二列,经历利率调整预期之后,是怎样对expected duration产生影响的,之间的传导机制是怎么样的?”
利率的改变,债券的Duration一定会发生变化。
咱们学过Duration是通过求利率债券价格公式的一阶导算的。假设是三年期的债券,有利率价格公式:
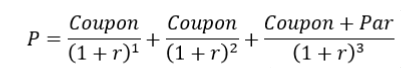
求Duration,需要对上面的公式求导,则有:

上面求导后的公式,是求债券Duration公式的主体部分。
所以可以发现债券的Duration是利率的函数,当利率发生改变时,债券的Duration数据也会变化。
所以对于这个Initial Portfolio,经历一个0.60%的收益率曲线改变,债券的期末(At the horizon)Duration一定会发生变化。
这就是从表格中的1.313变到了1.305.
上面公式里的负号,仅仅是代表利率变动与债券价格呈现反向关系,我们把负号拿掉,就会发现当利率上升时,算下来的数值变小,即Duration变小。
这也对应表格里的数据,Initial portfolio,经历了一个0.60%的利率上升后,Duration变得更小了。
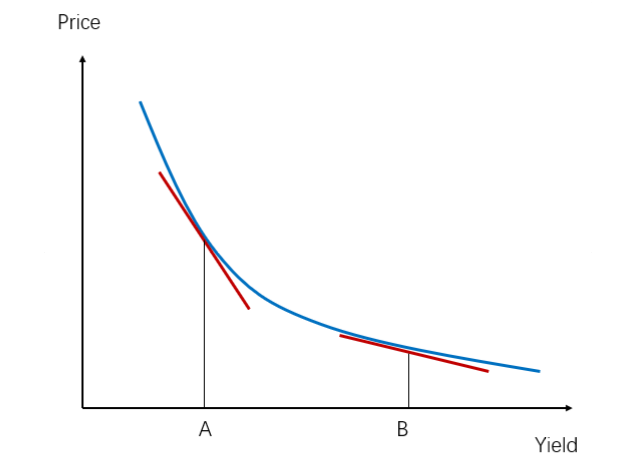
或者简单看这个Price-Yield关系图,Duration就是曲线上的切线,当横轴的利率改变时,对于曲线上的切线一定会变,也就是利率变化时,债券的Duration一定会变。比如,利率上升时,债券的Duration一定下降,因为切线更平坦,代表利率的敏感度(Duration)更低了。
这也对应表格里的数据,Initial portfolio,经历了一个0.60%的利率上升后,Duration变得更小了。
发亮_品职助教 · 2019年12月28日
第一列就是初始Portfolio的数据,是初始的静态数据;
第二列就是用这个初始Portfolio,经历一下利率预期变动之后,反映出的组合数据。
第三列就是改变组合Position之后,经历一下利率预期变动之后,反映出的组合数据。
所以反映出来的差别就主要体现在Duration上,因为预期利率是上升的,所以调整之后的组合,也就是第三列Portfolio算下来的表现肯定更好,因为他的Duration比第二列未调整组合的Duration更小。
所以第二列是用来和第三列比较的。
第一列其实没啥用,只能算假设利率不变的情况下,Portfolio的收益。
粉红豹 · 2019年12月28日
那么请教下,对于第二列,经历利率调整预期之后,是怎样对expected duration产生影响的,之间的传导机制是怎么样的?