
发亮_品职助教 · 2019年10月12日
凸性描述的就是债券价格与收益率曲线之间的非线性关系,如下图这种曲线关系:
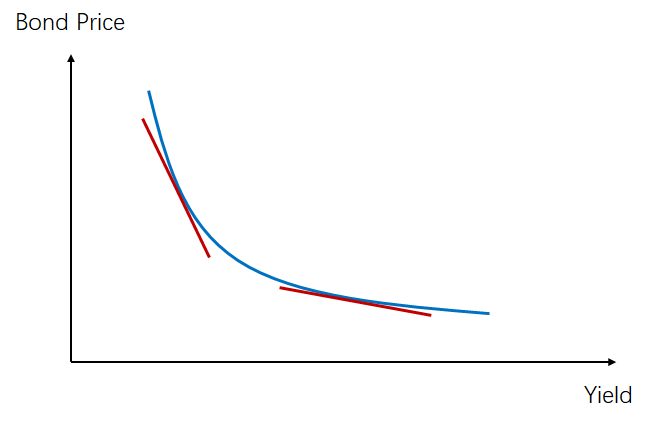
但当收益率曲线发生小幅变动时,这种曲线的关系,可以近似地用切线线性来表示,所以我们就只用Duration来衡量债券价格对利率的线性敏感度;
但是当收益率曲线发生大幅变动时,用切线来衡量影响误差就会变大,所以除了Duration外,再引入Convexity,一起来衡量利率变动对债券价格的影响;
相比只考虑切线Duration,引入Convexity之后,发现Convexity总是有利的,因为当利率降低时,引入Convexity后衡量的债券价格上升幅度更大,曲线在切线(只有Duration线性衡量)的上面;
而当利率上升时,引入Convexity后衡量的债券价格下降幅度更小,因为曲线在切线的上面。
所以凸性,就是这种非线性关系带来的。
这种非线性关系,在Option里面也有,对应的Option的Delta衡量线性关系,类似Duration,Option的Gamma衡量非线性关系,类似Convexity。
以标的物是债券的Call Option为例,当债券价格下降时,Option价值下降,但Option价值下降幅度更慢,因为当标的物债券价格下降至行权价之下时,Option的价值已经为零,标的物债券价格继续下降将不太影响Option的价值,这种Option价值下降速度相比标的物债券更慢就是Convexity属性里的“跌少”;
当债券价格上升时,尤其是债券价格上升至行权价附近时,债券价格的继续上涨会带来期权价格的急速大幅上涨,因为期权即将进入At-the-money;使得Option的Delta由0.5急速上升至1,即:Option的价值与标的物价值的变动呈现1:1的关系;
而衡量Delta变动速度的就是Gamma,也就是Option的非线性关系,推动Option价值加速上涨,这就是Convexity属性里的“涨多”;
所以Option呈现Convexity的特性,可以利用Option来调节债券组合的Convexity数据;
Convexity不是免费的,因为Convexity大的债券,要求现金流更分散,即Coupon、期间现金流较高,这种债券往往更受欢迎,买价较高(或者持有至到期收益YTM较低),相比类似的债券,较低的YTM就是为Convexity付出的成本。
Option也是一样,其他条件类似,At-the-money附近的Option,售价也较贵,为了获得非线性涨多跌少需要付出较高的期权费用。如下图,是原版书给出的Call option on bond与Bond price之间的非线性图:
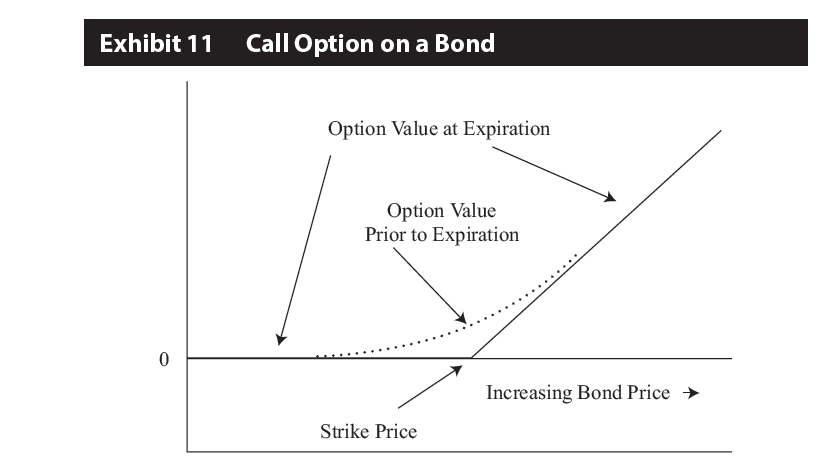
总结下:利用Option调节Convexity,就是因为Option价格和标的物价值之间存在非线性关系;为了获得Option带来的非线性关系,需要花钱购买Option,这是付出的成本