不理解equity option的波动率微笑曲线的两个原因

@棉花糖同学，不是按你的这个角度理解的，我说的这些是原版书的解释。

对于OTM的put而言（其行权价为K1），P{SP{S，是大于理论情况下也就是Lognormal distribution下的P{S的 。所以真实情况下，OTM的put的隐波会较贵，因此，当K较小时，隐波会较高。

是按这个逻辑去想的

上面两张图的解释是从实证的角度来解释的，杠杆和崩盘恐惧症是从金融经济的角度来解释的，并且杠杆和崩盘带来的影响，也是和实证结论的相一致的。从杠杆和崩盘的角度，资产价格下跌的更严重，所以它资产价格的分布相比理论假设的lognormal 分布，左尾会更肥，这就对应着图二的左边情况。此时，put就会更贵，隐波也就更高。所以原版书说杠杆和实证图是consistent的

Figure17-3、17-4 就是我上面贴的两张图

同学你好，这里的逻辑原版书上讲的比较好。拿一个deep OTM 的 call举例，也就是对于这个看涨期权而言，它的行权价很高，为K2。

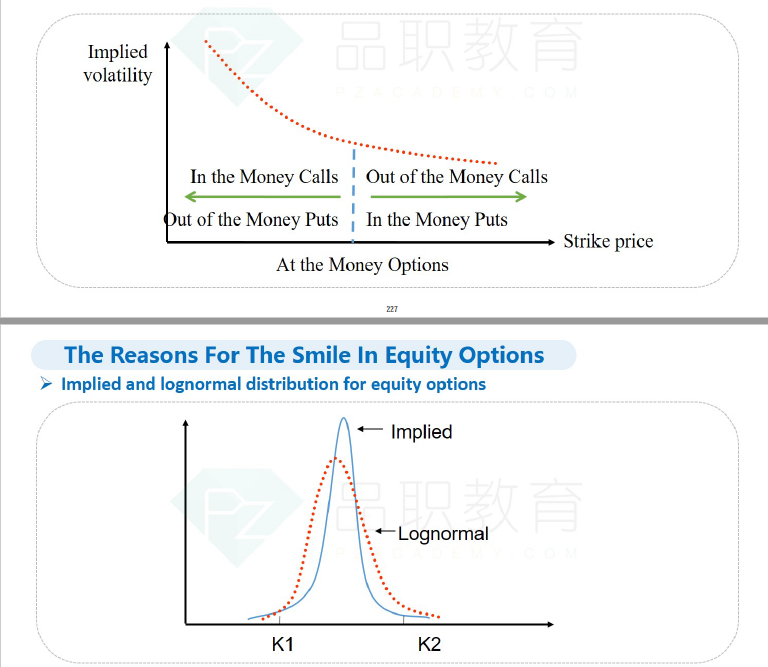
下图的第二个函数图像，它的横坐标是S。在这张图中，implied distribution 描述的是现实情况下，标的资产价格的密度函数。lognormal distribution是理论假设下的标的资产价格的密度函数。

对于这个看涨期权而言，它的行权价为K2，因此只有当S大于K2时，这个期权才会为投资者带来收益，也就是说，P{S>K2}的概率越高，这个期权就越值钱。而根据implied distribution和lognormal distribution，也就是根据真实情况下与理论情况下它的价格密度分布函数，我们可以看到，P{S>K2}的真实概率，是小于理论情况下P{S>K2}的概率的。也就是说，真实情况下的看涨期权，没有理论情况下的看涨期权值钱。而我们知道，期权的价格是和它的隐含波动率成正相关关系。因此，真实情况下，P{S>K2}的概率更低，看涨期权更不值钱，它的隐波也就越低。所以当行权价较高时，隐波较低。这解释了图一的右边为什么是行权价越高，隐波越低。

图一的左边同理。对于OTM的put而言（其行权价为K1），P{SP{S，是大于理论情况下也就是Lognormal distribution下的P{S的 。因此，当K较小时，隐波会较高。

杠杆、崩盘恐惧症，是从另一个角度解释了为什么标的资产价格下跌时，波动率会变高。