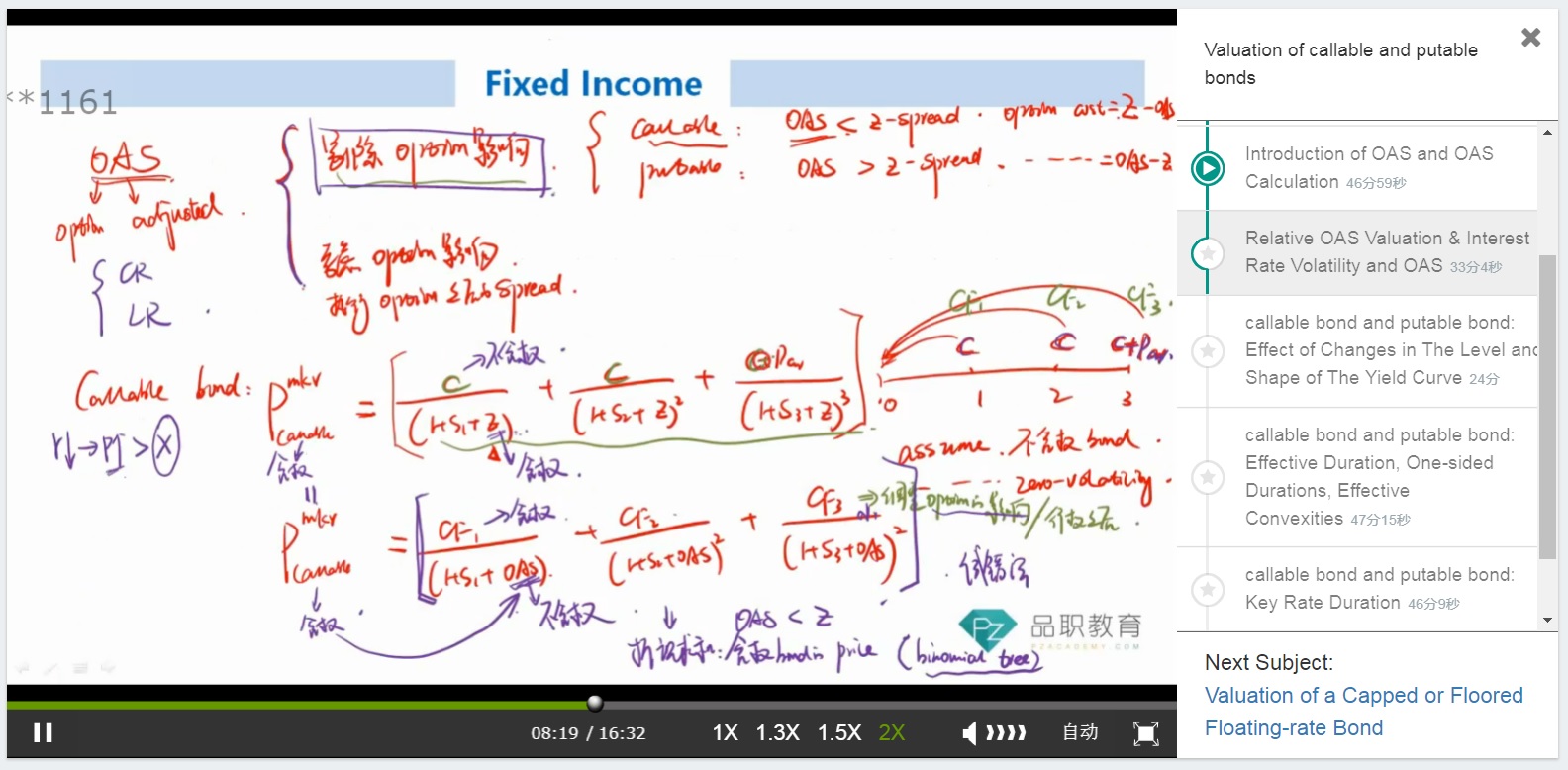
课件中何老师讲到callable bond的计算可以中z spread计算,其中分母没有考虑含权,是分子z包含了权利,那么后来讲到oas的时候又说z不受option变化的影响,我就不明白了,是不是前后不一致啊
发亮_品职助教 · 2019年03月13日
Z-spread是直接从Spot rate curve里面求出来的。不含利率的波动率的假设。
从Spot rate curve可以求出来Implied forward rate,在这个Implied forward rate的基础上,我们有一个利率波动率的假设,上下两个树杈出现两种可能的Forward rate,并且这两个树杈是以Implied forward rate为Middle rate展开的。
从上面这个过程中可以看出,利率的波动率是不影响Middle rate,即不影响Implied forward rate大小的(在我们CFA里面学到的是基本不影响),因为Spot rate和Implied forward rate反映同样的利率信息,所以Volatility也不影响Spot rate,进而不影响Z-spread.
发亮_品职助教 · 2019年03月04日
前后没有矛盾说的是一回事。
我们是通过对债券未来的现金流(1),合适的折现率折现(2),得到债券的合理价格(3)。
以上(1),(2),(3)任意知道2个,就可以求出另外一个。
在Spread这里,我们是知道债券的现金流和债券的价格,来反求出债券的折现率,从而得到债券的风险溢价Spread。
第一种方法求得的是Z-spread,由于是含权债券,而折现时直接用的是债券的Coupon rate,这个现金流是没有反应债券是否行权的风险;而债券的市场价格,是反映了投资者对债券所有风险的预期,这个价格是反映出了投资者投资该债券所承担的所有风险,所以用此时的该市场价格和债券Coupon,反求出来的Z-spread就反映了这支债券的所有风险。
而Callable bond,投资者承担的风险有:Credit risk + Liquidity risk + option risk,这里的Option risk,是投资者承担了债券被发行人提前赎回的风险。
因为投资者承担了以上的风险所以这里反求出来的Z-spread里面就反映了以上风险的补偿:
Credit spread + Liquidity spread + option "spread"
所以Z-spread是一个All in spread,债券里面有什么风险,就全部反映在Z-spread里面的。
所以这个Z-spread里面是反映了投资者承担被提前行权的风险,也就是Z-spread包含了权利的影响。
如果债券的风险太多,Z-spread就很杂,而投资者如果只想知道投资债券的Credit risk,就需要从Z-spread里面把“Option risk”的补偿剔除掉。
这个剔除掉权利影响后的风险补偿就是OAS(Option-adjusted spread)。
为了使得反求出来的折现率,只反映Credit risk,我们就需要把Option的风险反映在分子的现金流里,这个风险就是权利对债券现金流的影响;所以在求OAS时,分子的现金流,我们是对权利是否行权进行过调整的。这种反求出来的折现率OAS,是不包括对权利补偿的(Option risk),因为风险都反映在分子现金流里面了,那么求出来的Spread(OAS),就全部只反映Credit spread。
所以这个OAS是剔除了债券权利影响后,只反映债券Credit risk的风险补偿。所以说OAS这个Spread里面不反应权利的影响,是剔除权利之后的Credit spread。