
发亮_品职助教 · 2019年01月09日
Cash flow yield就是现金流的IRR概念;类比到债券,就是债券的YTM。
所以Semi-annual cash flow yield 类比就是Semi-annual YTM;
Annual cash flow yield 类比就是 annual YTM
对于一个半年付息一次的债券,我们知道购买价Price,知道未来的现金流:Coupon及其到期本金;
可以根据债券定价模型计算出折现率Semi-annual YTM
也就是可以算出一个IRR,即Semi-annual YTM
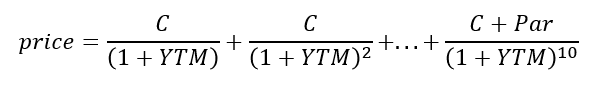
叫Semi-annual,是因为这是半年付息一次的债券,折现率是对半年发生一次的现金流折现,所以分母是Semi-annual YTM,乘以2之后得到Annual YTM;
这个Annual YTM就是我们常说的债券YTM;
Annual Cash flow yield就是类比为债券的Annual YTM;Semi-annual Cash flow yield,就类比于债券的Semi-annual YTM,也就是分母上的折现率;
为什么本例题我们不直接求债券的YTM,而是求Cash flow yield;
因为这是一个Bond Portfolio,组合内的债券有不同的到期日,有不同的Coupon rate,所以我们把所有债券在每一个时期发生的现金流相加,得到Portfolio在每一个时期的现金流,于是这个Portfolio就看成是一个现金流更大的Bond,这个Bond在每一个时期的现金流就是各成份债券在该时期现金流的汇总。
我们知道构建这个Portfolio的价格,利用同样的折现方法对每一期的现金流折现,反算出折现率IRR;
算出来的折现率就是Semi-annual Cash flow yield;因为是半年付息一次,所以乘以2就是Annual Cash flow yield;
和对债券现金流折现一样,对于半年发生一次的现金流折现,只使用Semi-annual Cash flow yield。
视频里面讲到的1.8804就是分母的折现率,即Semi-annual Cash flow yield
如果是给定一个真正的半年付息一次的Bond,要算Convexity,要用到Semi-annual YTM,就是单期YTM;
因为我们把这个Portfolio当做了一个现金流更大的Bond,算Convexity的公式就用到了单期Cash flow yield;即Semi-annual cash flow yield.
发亮_品职助教 · 2019年01月11日
他这个Precise Cash flow yield出现在这里,如下图:
用求IRR的方法算出来的CFY是:1.88037819%;这是精确值就是Precise CFY;
但是题目在折现现金流的时候取了近似值:1.8804%,也就是用了这个数折现;
这是折现率,出现在分母上的时候还要加1再次方,所以关于Precise CFY那句:
关于最后一句标黄说的1.0188037819%,就是分母的(1+1.88037819%);1.88037819%就是Precise CFY

关于为什么计算债券组合的数据要用Cash flow yield,见上一个回复;
以下是如何计算Cash flow yield:
Cash flow yield,就类比成债券的YTM,是分母上对现金流的折现率,也就是IRR概念。
对于债券持有至到期收益率,有YTM概念;
而债券组合因为每一个成份债券的到期不一样,所以持有组合的到期收益率,定义为:Cash flow yield;
债券组合的Cash flow yield计算方法和单个债券计算YTM的方法一致。
原版书上这个Example,他构建了一个Portfolio,而Portfolio有3个不同的债券构成。如下图:

这个Bond portfolio可以看成一个大的债券,比如构建好债券组合之后,半年之后会收到三笔现金流,分别为:
2.5-year bond的第一笔Coupon,352,500;7-year bond的第一笔Coupon,1,581,125;10-year bond的第一笔Coupon,1,390,000,这一期总现金流为:3,323,625;
依照这个办法,把每一期现金流相加得到组合每一期的现金流;于是这个组合就可以看成一个现金流更大的债券。
组合现金流分布如下:
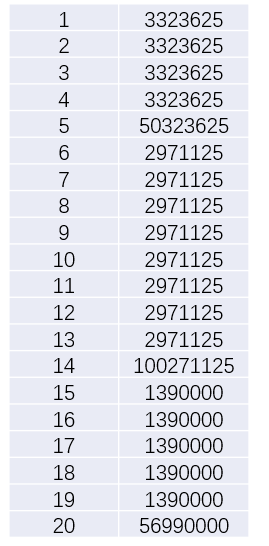
组合期初的购买价格为:47,117,500+97,056,750+55,878,000=200,052,250
这是构建组合的成本,也购买这个大债券的价格;按照求债券YTM的方法,我们求组合的Cash flow yield:

分母就是我们要求的Cash flow yield,发现这个和求单个债券YTM的方法一致。
所以单个债券求各项数据如果用到了YTM,类比到债券组合,就要用Cash flow yield.