课件中讲到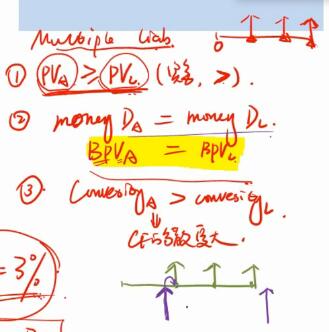
为了第一笔现金流在债务之前到账,在久期相同的情况下,assets最后一笔现金流应该比liability 更晚,assets lisai离散程度和convexity应该更大,那么所有债务到期情况下,assets还没有完全收回,这样不就无法还清债务了吗?
发亮_品职助教 · 2018年12月11日
在Match Multiple liability时,要求的是Asset convexity大于Liability convexity这点没错。
在债务到期时,Maturity更长的债券,是提前卖出,以偿还负债。所以不存在你说的Asset还没有完全收回,无法满足负债的情况。
回想一下,再构建单期负债匹配策略时,其中免疫的一个要求就是:
Investment horizon (Liability maturity) = Asset Macaulay duration。
因为当满足这个条件时:Coupon的再投资风险,与负债到期时提前卖出资产的价格风险相互抵消,使得债券在这个投资期获得一个稳定的收益,实现稳定的增值到期Cover负债。所以,是债务到期时,需要卖出债券来Cover liability。
多期负债可以看成是多个单期负债的叠加,如下图,1,2,3的位置上三笔红线代表三笔负债:一个多期负债未来1,2,3年,年末各有一笔负债需要偿还,但是可以看成是由3个单期负债组合起来的。所以,我们以单期负债为例,多期的情况可以类比。
只看第一年到期的负债,如下图,如果要用Bond portfolio匹配该负债,尽可能完美的匹配,需要我们构建的Portfolio尽可能的模拟1年期的零息债券。这个Portfolio需要满足资产的Macaulay duration = 1,并且资产的Convexity最小,也就是尽可能地模拟1年期的零息债券。
满足这个条件一定是如下图所示,Bond portfolio的现金流在1的左右两侧,紧贴着1,如蓝线。这个是在Macaulay duration match情况下,使得Convexiy最小的分布。也是最优的模拟1年期零息债券的情况。

将多期负债看成多个单期负债的组合,为了满足多期负债,类比一下,如下图所示,呈现这样的情况:

只看两端最外层的现金流,就是你上传的这个图。显然资产的现金流“包裹”住了负债的现金流(就使得Asset的Convexity大于Liability的Convexity),这已经满足了匹配的要求;
如果资产的现金流越紧贴负债现金流(Asset的Convexity在大于Liability convexity的情况下,尽量靠近Liability Convexity),匹配的效果越好。
以上是另一个思路帮助理解,记住匹配条件是关键。