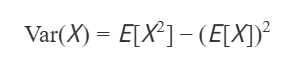Emily晓华 · 2025年05月12日
09:02 (1.5X)
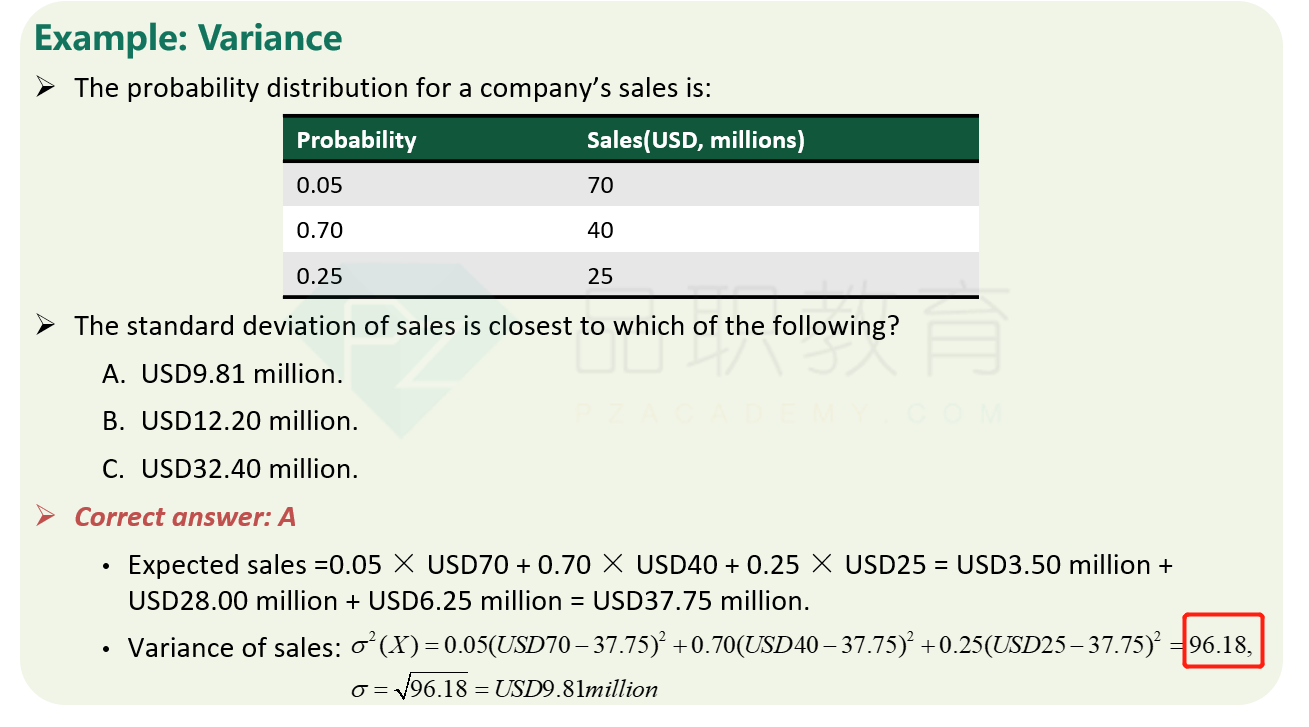
请问何老师这里讲的这个变形的（方差=平方的期望-期望的平方）公式在计算中验证过吗？感觉这个式子不能反映出权重该算在哪里。我根据老师的这个公式直接把后面例题带进去算了是不行的。所以我觉得何老师这个推导在倒数第二步时在后面两项中要保留期望符号，然后在最后一步再把期望符号整体提出来，即E{(X^2)-[E(X)]^2}，这样在计算时把括号中相减的结果乘以权重。我按这个步骤用上面提到的同一个例题的数试了一下是对的。
请问老师我的理解对吗？还是说何老师推导出的公式本来就是这样的，只是我理解错了？因为我对这些知识完全是小白，但觉得老师的这些推导很有意思，所以就试了一下。没有别的意思。
品职助教_七七 · 2025年05月12日
嗨，从没放弃的小努力你好：
同学你好，
这个公式确定是没问题的。
对于这道题：
1）根据图表第二列，X分别为70，40，和25，所以对应的X平方分别为 4900,1600和625.
E(X的平方)为对 X的平方 以概率为权重做加权平均，结果为 0.05 × 4900 + 0.70 × 1600 + 0.25 × 625 =1521.25。
2）E(X)=0.05 × 70 + 0.70 × 40 + 0.25 × 25 =37.75，所以E(X)的平方等于37.75的平方，即1425.0625
所以根据何老师写的公式，方差应为第一步算出的1521.25减去第二步算出1425.0625，1521.25-1425.0625=96.1875。和答案给出的96.18是一样的。
可以将上述过程和自己的计算进行对照，分析一下为什么代进去算了不行，差在哪一步。也可以把自己的算法贴上来，对比一下看问题出在哪。
----------------------------------------------
虽然现在很辛苦，但努力过的感觉真的很好，加油！
