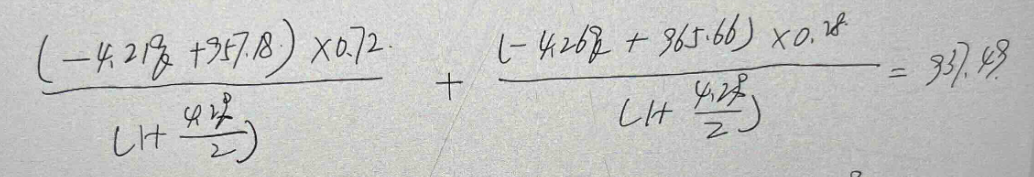NO.PZ2023100703000129
问题如下:
An analyst on the fixed-income desk at Bank PNMS has been asked to complete the construction of a zero-coupon bond price tree that was started by another team member. The analyst is given an interest rate tree of semi-annual spot interest rates quoted on an annualized basis, and the partially completed price tree, both with semi-annual time steps, as shown below (time t in years and price P in USD):
When completing the price tree, which of the following is a correct estimate of price P(1,1)?
选项:
A.
USD 954.15
B.
USD 954.81
C.
USD 956.25
D.
USD 956.92
解释:
B is correct. For a full example see page 160. The analyst first needs to solve for q using the following system of equations:
Equation 1: (0.72*P1,1 + 0.28*P1,0) / (1 + 0.042/2) = 937.489
Equation 2: (975.13q + 979.43(1-q)) / (1 + 0.0465/2) = P1,1
Equation 3: (979.43q + 983.77(1-q)) / (1 + 0.0375/2) = P1,0
Substituting equations 2 and 3 into equation 1 allows for q to be solved for, yielding a result of q=0.563.
Then to find P1,1, the value of q can be substituted back into equation 2.
(975.13*0.563 + 979.43*(1-0.563)) / (1 + .0465/2) = (548.998 + 428.011) / (1.02325) = 954.81
A is incorrect. The probabilities of up and down moves given in the rate tree are incorrectly used as values for q and 1-q.
(975.13*0.72 + 979.43*(1-0.72)) / (1 + .0465/2) = (702.094 + 274.24) / (1.02325) = 954.15
C is incorrect. The probabilities of up and down moves given in the rate tree are incorrectly used as values for q and 1-q AND the interest rate at the initial node is incorrectly used as the discount rate.
(975.13*0.72 + 979.43*(1-0.72)) / (1 + .042/2) = (702.094 + 274.24) / (1.021) = 956.25
D is incorrect. The interest rate at the initial node is incorrectly used as the discount rate.
(975.13*0.563 + 979.43*(1-0.563)) / (1 + .042/2) =
(548.998+428.011) / (1.021) = 956.91

老师好,这个计算过程哪里错误了呢?