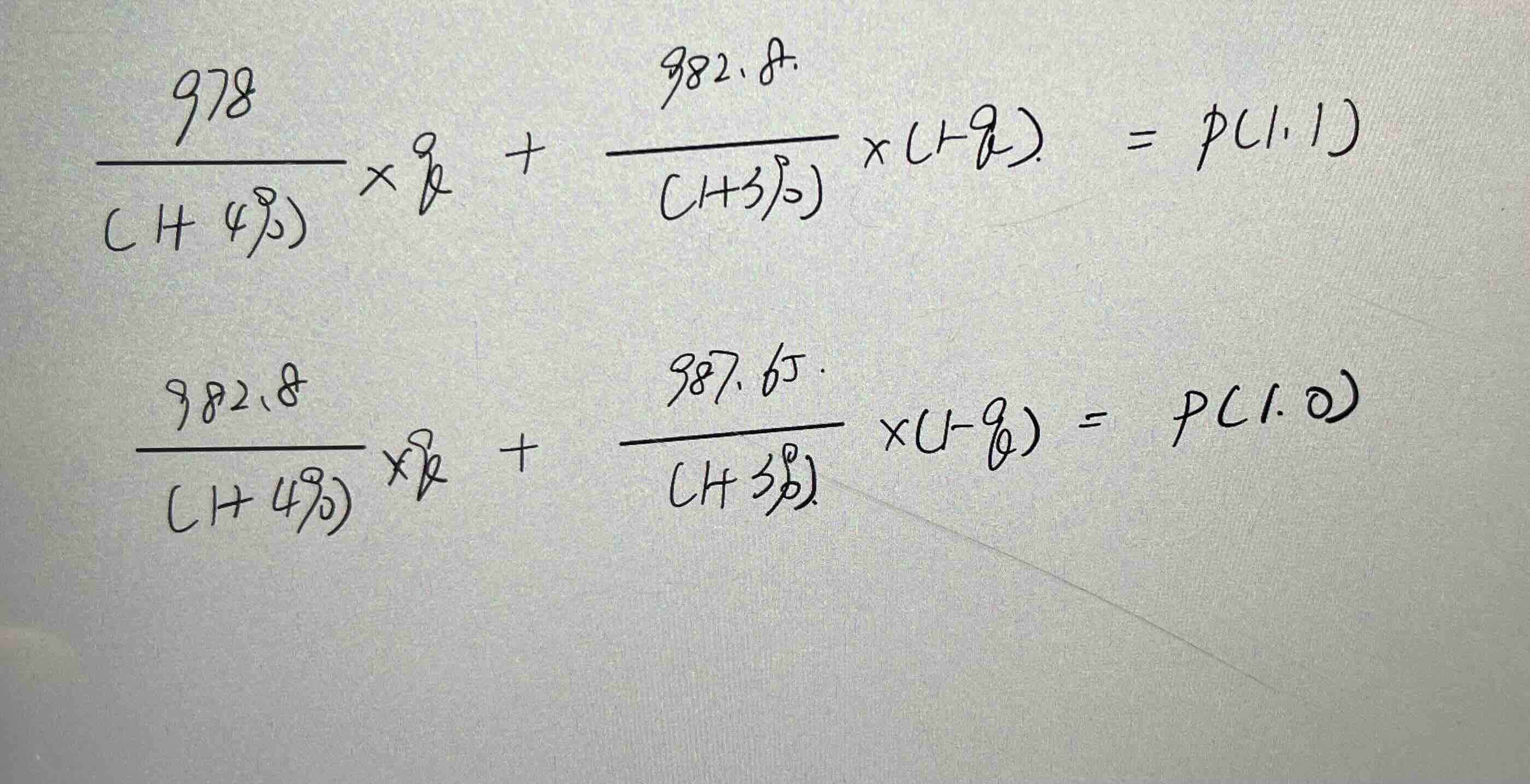NO.PZ2023100703000133
问题如下:
An analyst
on the fixed-income desk of an investment bank is calculating the risk neutral
probabilities of upward or downward movements in interest rates at various
nodes in a zero-coupon bond price tree. The analyst constructs an interest rate
tree of semi-annual spot interest rates quoted on an annualized basis, and a
price tree, both with semi-annual time steps, as shown below (t in years)
What is the
risk-neutral probability of the upward movement labeled q?
选项:
A.
0.15
B.
0.50
C.
0.70
D.
0.85
解释:
D is
correct. From the given rate tree and price tree, the equation for the price of
a 1.5-year zero-coupon bond at t = 0 is:
Equation 1:
(0.7 * P(1,1) + 0.3 * P(1,0)) / (1 + 0.035/2) = 945.80
and the
prices for the then 1-year bond at t = 0.5 are:
Equation 2:
P(1,1) = (978.00q + 982.80(1-q)) / (1 + 0.04/2)
Equation 3:
P(1,0) = (982.80q + 987.65(1-q)) / (1 + 0.03/2)
Substituting
Equations 2 and 3 into Equation 1 allows for q to be solved for algebraically,
resulting in q = 0.85.
A is
incorrect. This is the risk-neutral probability of a downward movement.
B is
incorrect. This incorrectly assumes that risk-neutrality indicates a
probability of ½.
C is incorrect. This assumes that the risk-neutral probability of an upward movement at t = 0.5 is equal to the risk-neutral probability of an upward movement at t = 0. As shown in the text, this is not the case.
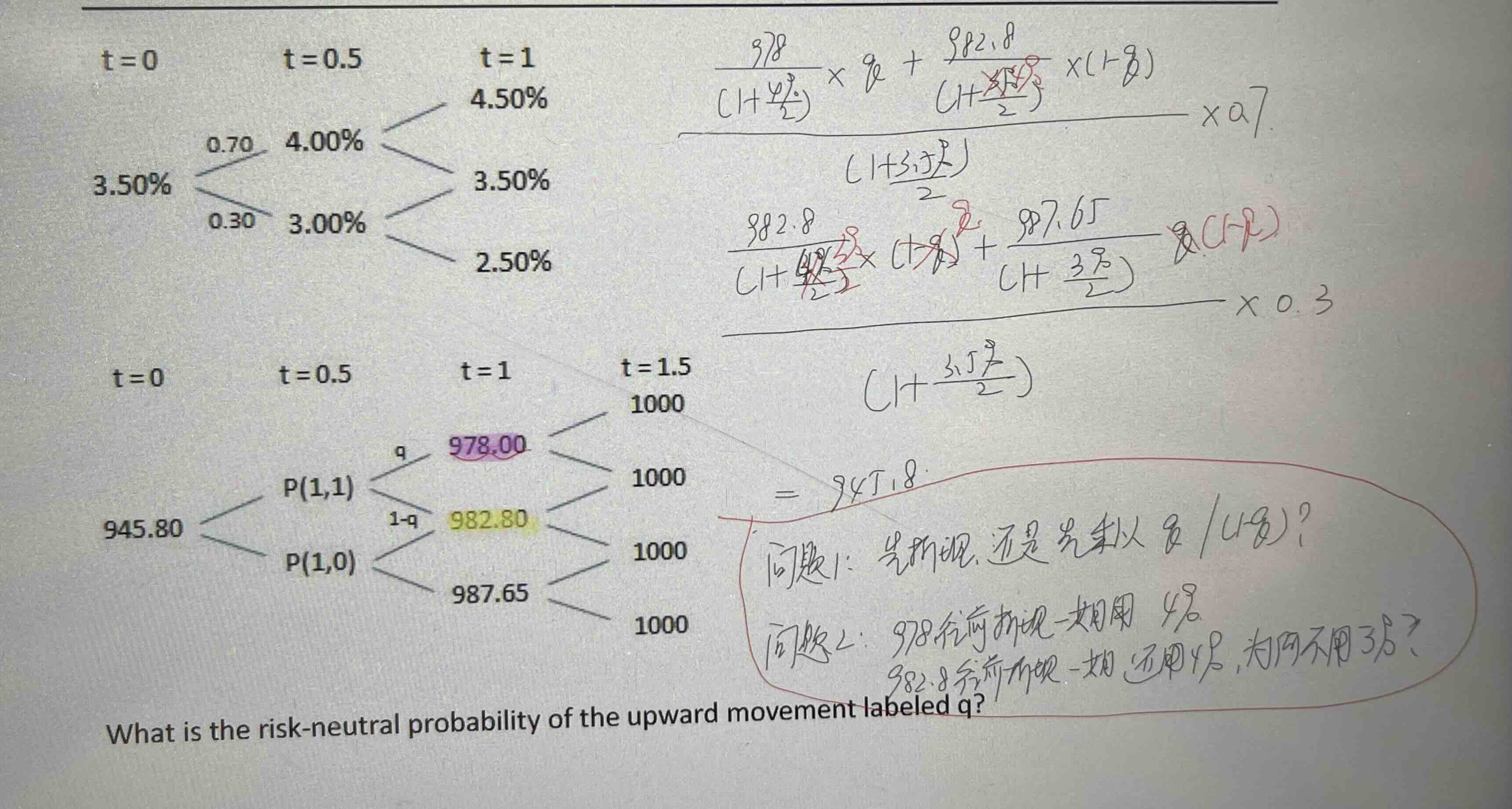
老师,问题1,无论是求债券价格(不含权和含权)还是期权价格,到底是先折现再乘以概率,还是先乘以概率再折现?
问题2,982.8是价格下降,为什么还是用4%折现,不是3%?不应该是: