NO.PZ2022071105000019
问题如下:
A fund manager owns a portfolio of options on TUV, a non-dividend paying stock. The portfolio is made up of
5,000 deep in-the-money call options on TUV and 20,000 deep out-of-the-money call options on TUV. The
portfolio also contains 10,000 forward contracts on TUV. Currently, TUV is trading at USD 52. Assuming 252
trading days in a year, the volatility of TUV is 12% per year, and that each of the option and forward contracts is
on one share of TUV, which of the following amounts would be closest to the 1-day 99% VaR of the portfolio?
选项:
A.
USD 11,557
B.
USD 12,627
C.
USD 13,715
D.
USD 32,000
解释:
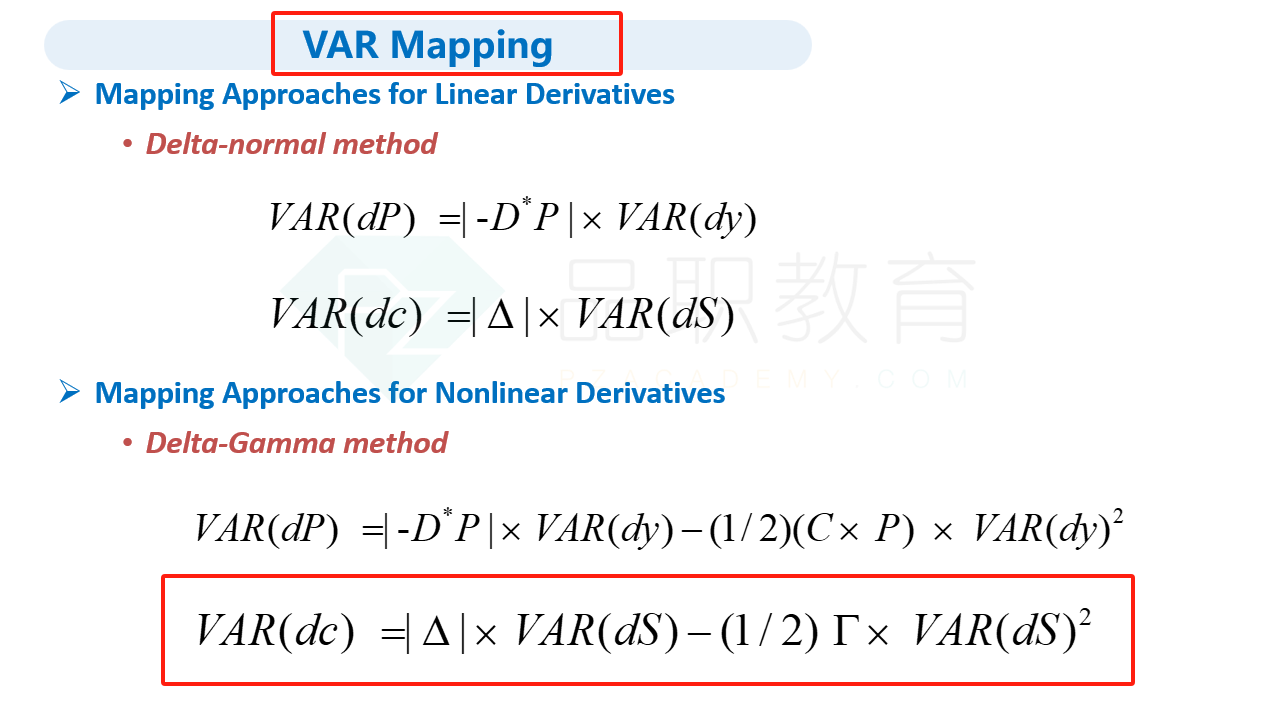
C是正确的。我们需要把资产组合map到股票TUV上面。一个深度实值看涨期权的delta接近于1,深度虚值看涨期权的delta接近于0, 一份远期合约的delta等于1。
所以资产组合的delta(Dp) = 1*5,000 + 0*20,000 + 1*10,000 = 15,000, 并且资产组合是gamma中性的。
现有:
ꭤ = 2.326 (99% 置信度)
S = TUV的股价 = USD 52
Dp = 资产组合的delta = 15,000
σ = TUV股票的波动率 = 0.12
所以99%置信度水平下的1天的VaR等于:
ꭤ *S*Dp*σ*sqrt(1/T) = (2.326)*(52)*(15,000)*(0.12/sqrt(252)) = USD 13,714.67
C is correct. We need to map the portfolio to a position in the underlying stock TUV. A
deep in-the-money call has a delta of approximately 1, a deep out-of-the-money call has a
delta of approximately zero and forwards have a delta of 1.
The net portfolio has a delta (Dp) of about 1*5,000 + 0*20,000 + 1*10,000 = 15,000 and is
approximately gamma neutral.
Let:
ꭤ = 2.326 (99% confidence level)
S = price per share of stock TUV = USD 52
Dp = delta of the position = 15,000
σ = volatility of TUV = 0.12
Therefore, the 1-day VaR estimate at 99% confidence level is computed as follows:
ꭤ *S*Dp*σ*sqrt(1/T) = (2.326)*(52)*(15,000)*(0.12/sqrt(252)) = USD 13,714.67
这里计算过程涉及的知识点是哪个