NO.PZ2024120401000013
问题如下:
You collect 50 years of annual data on equity and bond returns. The estimated mean equity return is 7.3% per year, and the sample mean bond return is 2.7% per year. The sample standard deviations are 18.4% and 5.3%, respectively. The correlation between the two-return series is -60%. Are the expected returns on these two assets statistically significantly different from each other(assume the size is 5%)?
选项:
A.They are significantly different from each other. B.They are not significantly different from each other.
C.Cannot decide whether they are significantly different.
解释:
The null hypothesis is H0: μE=μB. The alternative is H1: μE≠μB. The test statistic is based on the difference of the average returns, δ=7.3%-2.7%=4.6%.
The estimator of the variance of the difference is:
which is 0.1842 +0.0532 -2*(-0.6)* 0.184*0.053=0.0484.
The test statistic is:
δ / sqrt(0.0484 / 50) = 1.478.
The critical value for a two-sides test is ±1.96 using a size of 5%. The null is not rejected. If the correlation was 0, then the variance estimate would be 0.0366, and the test statistic would be 1.70. The null would still not be rejected if the size was 5%.
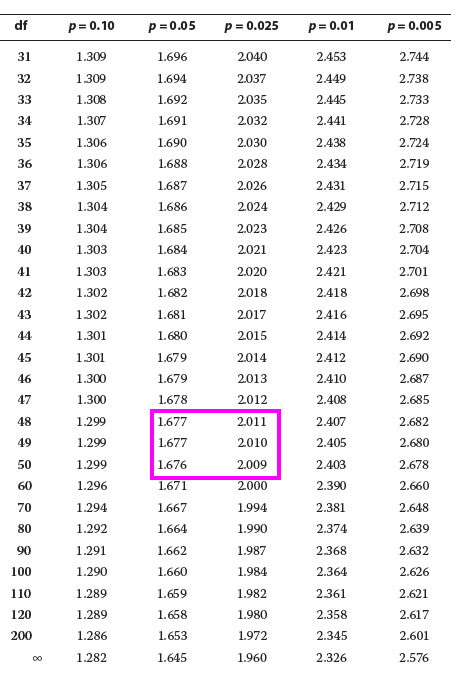
解析说:The critical value for a two-sides test is ±1.96 using a size of 5%. The null is not rejected. If the correlation was 0, then the variance estimate would be 0.0366, and the test statistic would be 1.70. 这里不管ρ是否等于零,这个1.7是取错了吧?
既然是双尾拿对应的应该是df=48,0.025(这个t分布表为单尾)——2.011?
虽然结论是不变的,落在拒绝域里面。



