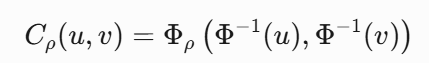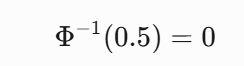NO.PZ2020011303000130
问题如下:
X and Y are variables that have uniform distributions between 0 and 1 (a uniform distribution is a distribution where all values in a certain range are equally likely). A Gaussian copula model is used to define a correlation
选项:
A.
0.20
B.
0.25
C.
0.29
D.
0.33
解释:
In the Gaussian copula model, the 0.5 values for X is transformed to the zero value of a standard normal distribution. The same is true for Y. The required probability is the probability that the first variable is less than zero, and the second variable is less than zero in a bivariate normal probability distribution where the coefficient of correlation is 0.25 (it can be shown that this is about 0.29).
题目问:X 和 Y 是在 0 和 1 之间具有均匀分布的变量(均匀分布是某个范围内的所有值的可能性均等的分布)。高斯 copula 模型用于定义它们之间的相关性。相关参数为 0.25。如何确定两者都小于 0.5 的概率?
在高斯 copula 模型中,X 的 0.5 值转换为标准正态分布的零值。对于 Y 也是如此。 在相关系数为 0.25 的二元正态概率分布中,所需的概率是第一个变量小于零,第二个变量小于零的概率(约为 0.29)。
虽然看老师说超纲了,但既然放这里了就很好奇到底怎么做的,我完全没思路。