equity

问题如下：

The Epsilon Institute Case Scenario

The Epsilon Institute of Theoretical Physics is a non-profit corporation initially funded from government and private sources. Mitch Lazare is the chairman of the Investment Committee, which oversees the institute’s endowment fund, of which about $750 million is currently under active management. He is currently tasked with finding two additional investment managers to manage a portion of the actively managed funds and, along with his assistant, Brian Warrack, is reviewing the presentations made by several applicants.

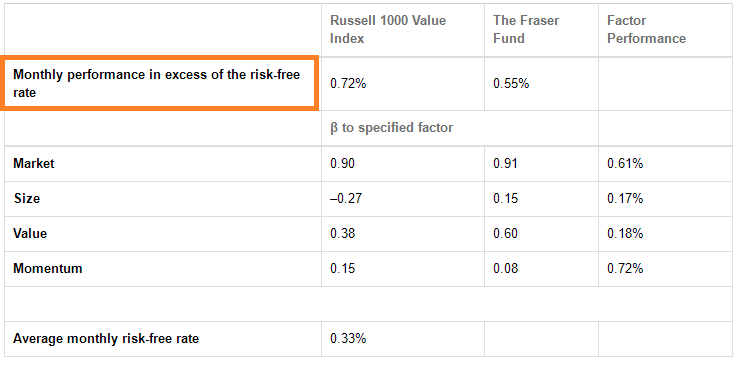
John Fraser’s performance is the first that Lazare and Warrack review. Fraser’s fund is constructed with a discretionary approach using the four Fama–French factors; he uses the Russell 1000 Value Index as his benchmark. The most recent 10 years of performance data for both the fund and the benchmark are shown in Exhibit 1.

Exhibit 1

Fraser Fund and Benchmark Average Monthly Performance over the Past 10 years

As part of his evaluation of the applicants, Warrack compiles a record of the Active Share and active risk of the funds that they manage. He observes that the Mattley Fund has relatively high Active Share but relatively low active risk.

Lazare and Warrack make the following comments about Active Share and active risk in the context of a single-factor model:

• The level of active risk will rise with an increase in idiosyncratic volatility.

• The active risk attributed to Active Share will be smaller in more diversified portfolios.

• If the factor exposure is fully neutralized, the Active Share will be entirely attributed to the active risk.

The manager of the Western Fund focuses on smaller companies in the Russell 1000 Value Index and uses the following constraints:

• Size: The capitalization of the average company is $1.8 billion. On average, companies of this size trade 0.90% of their capitalization every day.

• Liquidity: Positions can be no larger than 7% of average daily trading volume.

• Allocation: Positions can be no larger than 1.75% of total assets under management.

• Diversification: The portfolio must contain at least 60 securities.

If the manager of the Western Fund is hired by Epsilon, she will have $100 million of Epsilon’s funds to manage.

Lazare and Warrack turn their attention to the manager of the Herrick Fund, which is the only fund that involves substantial international exposure. Lazare believes that current political events in Country A may result in greater risk exposure than might be appropriate and wishes to investigate further.

The Herrick Fund manager provides them with the information in Exhibit 2, which they use to carry out a risk attribution analysis.

Exhibit 2

The Herrick Fund—Risk Analysis

Question

Using Exhibit 1, the average monthly return of the Fraser Fund that is unexplained by rewarded factors is closest to:

选项：

A.–0.20%. B.–0.17%. C.0.13%.

解释：

Solution

A is correct. Return from unrewarded factors = Actual monthly performance – Return from rewarded factors.“Alpha” = R_A – ∑β_pkF_kwhere

R_A = Actual portfolio performance

β_pk = The sensitivity of the portfolio (p) to each rewarded factor (k)

F_k = The return for each rewarded factor

Return from rewarded factors = (0.91 × 0.61%) + (0.15 × 0.17%) + (0.60 × 0.18%) + (0.08 × 0.72%) = 0.75%.

“Alpha” = Return from unrewarded factors = 0.55% – 0.75% = –0.20%.

B is incorrect. This is the “active return”: Actual – Benchmark = 0.55% – 0.72% = –0.17%.

C is incorrect. This adds the risk-free return back to the rewarded factor return = 0.33% – 0.20% = 0.13%.

中文解析：

本题考查的是主动投资收益来源的计算。

题目让我们根据表格给出的数据计算Fraser基金的主动投资收益中不能被rewarded factors解释的部分。

根据公式我们知道：

R_A =基金总的超额收益=0.55%

(α + ε)=不能被rewarded factors解释的超额收益

(α + ε)= R_A – ∑β_pkF_k，

∑β_pkF_k =可以被rewarded factors解释的超额收益=(0.91 × 0.61%) + (0.15 × 0.17%) + (0.60 × 0.18%) + (0.08 × 0.72%) = 0.75%.

因此，(α + ε)= R_A – ∑β_pkF_k = 0.55% – 0.75% = –0.20%，选项A正确。