为什么不能仅用convexity来表达上图中想呈现的“涨多跌少”的特征？

嗨，从没放弃的小努力你好：

你好老师，convexity代表着yield与price之间关系的曲线凸向原点的程度，它有着“涨多跌少”的特征，但是不能表达“利率变动百分率与价格变动百分率”之间的关系；而modified duration尽管能够表达两者（yield与"Δp/p"）的关系，但却是一条直线，不能很好体现“涨多跌少”的曲线特征，曲线也更接近真实情况。因此，我们将两者结合，兼顾变动率关系与涨多跌少。这样理解对吗？

Hello，亲爱的同学~

关于凸性，利率百分比与价格百分比之间的关系，受凸性的影响较小，凸性主要是表达涨多跌少的特点。所以，近似的来看，同学的这个理解，大致是正确的。

关于久期的理解，同学的说法是完全正确的。

这里也可以从公式来理解：

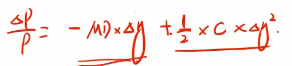
这个公式就表达了利率变动即与价格变动即的关系。

从公式可以看出，关于凸性的部分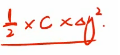，这个数值，是远远小于久期部分即这个数值的。

----------------------------------------------
就算太阳没有迎着我们而来，我们正在朝着它而去，加油！

嗨，努力学习的PZer你好：

既然convexity本身就代表了凸向原点的一条curve，那为什么不能就用它来表达上图中想呈现的“涨多跌少”的特征

Hello，亲爱的同学~

如果只是想表达涨多跌少的特征，那么看convexity确实是可以的。

而是要搞个“modified duration”和“convexity”的复合公式呢？

这里并不是只想表达涨多跌少。

而是想表达，收益率变动1%后，价格会变动多少。

价格与收益率的关系，仅仅一个凸性是不够的，还要看久期。

我理解，convexity本身就比modified duration更贴切地呈现了YTM和price之间的关系变化。

准确来说，convexity只反应涨多跌少的特征。

convexity和久期，共同反应，收益率与价格的关系。

对于以上答疑服务，同学只要有任何不理解的地方，都是可以随时继续追问的。

祝学习顺利，逢考必过~

----------------------------------------------
虽然现在很辛苦，但努力过的感觉真的很好，加油！