NO.PZ2015120604000145
问题如下:
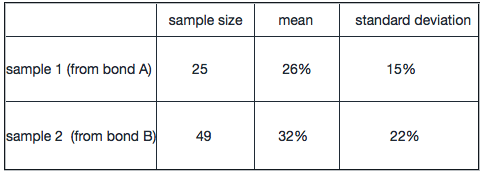
Here is a table discribing sample statistics from two bonds' rate of return which are both normally distributed over the past decades. If an investor is considering whether the mean of bond A is equal to 22%,
which of the following conclusion is least appropriate (significant level=1%) ?
选项:
A.The null hypothesis can be rejected.
B.It is appropriate to use a two-tailed t-test.
C.The test statistic value is 1.333.
解释:
A is correct.
The null hypothesis:
Because the sample size is 25, which is less than 30, so it is appropriate to use the two-tailed t-test.
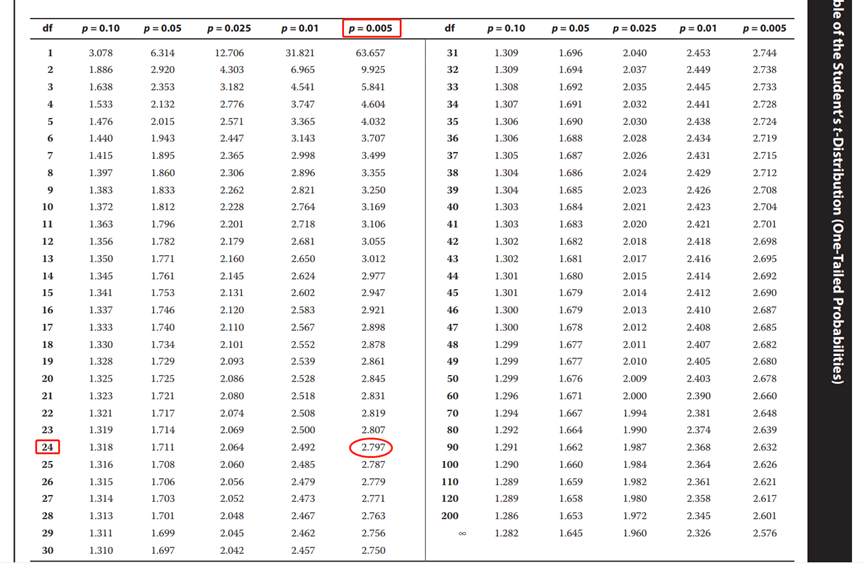
t at α= 0.01= ±2.797;
Because -2.797 <1.333<+2.797, therefore, H0 cannot be rejected.
请问: 考试这题怎么做?significant leval=1%, t检验是n-1. 这个考试中有表可以查吗?