NO.PZ2018123101000077
问题如下:
RW bond pays 4% coupon annually. It has a maturity of three years, and it is a callable bond that could be exercised at par at the end of years 1 and 2. To value and analyze RW’s bonds, Hsu uses an estimated interest rate volatility of 15% and constructs the binomial interest rate tree provided in Exhibit below:
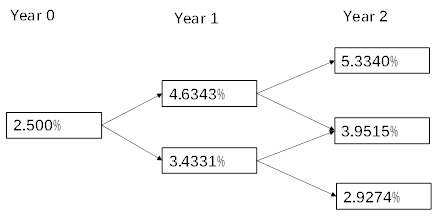
Rayes, a senior analyst, asks Hsu to determine the sensitivity of this callable Bond price to a 20 bps parallel shift of the benchmark yield curve. The results of Hsu’s calculations are shown in the table below:

The effective duration of RW’s callable Bond is closest to:
选项:
A.0.76.
B.1.88.
C.3.77.
解释:
B is correct.
考点:考察Effective duration概念
解析:
题干条件已经给定了Benchmark yield平行移动时,债券价格的变动,当Benchmark yield 上升20bps时,债券价格为100.478,当Benchmark yield降低20bps时,债券价格为101.238;根据有效久期的公式,可得有效久期为:
注意题干中并没有给定利率变动前的债券价格,即PV0(分母中的100.873),但是可以通过二叉树模型,计算出PV0。
如下所示:
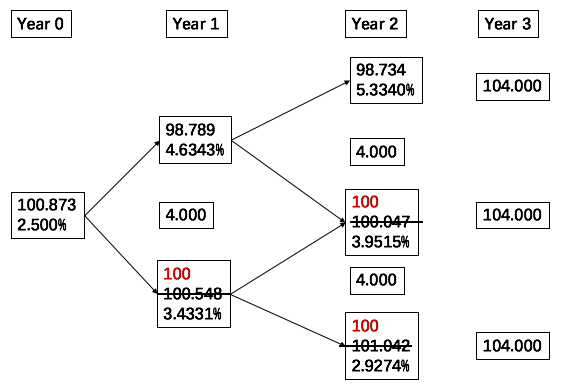
对比另一个题目NO.PZ2018123101000086中的解释如下:
没有call protection period的可债券在任何时刻都可以被call回(包括零时刻),所以零时刻的价格也无法超过100
如果本题没有说明可行权的时间,默认是按照期初也能行权的思路(即期初不能>100),还是期初不能行权的思路(即期初可以>100)呢?



