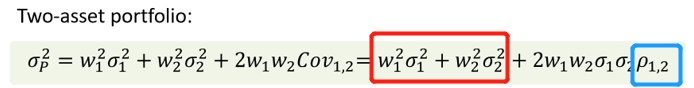NO.PZ2017092702000075
问题如下:
An analyst produces the following joint probability function for a foreign index (FI) and a domestic index (DI).

The covariance of returns on the foreign index and the returns on the domestic index is closest to:
选项:
A.
26.39%².
B.
26.56%².
C.
28.12%².
解释:
B is correct.
The covariance is 26.56, calculated as follows. First, expected returns are
E(RFI) = (0.25 × 25) + (0.50 × 15) + (0.25 × 10) = 6.25 + 7.50 + 2.50 = 16.25 and E(RDI) = (0.25 × 30) + (0.50 × 25) + (0.25 × 15) = 7.50 + 12.50 + 3.75 = 23.75. Covariance is
= 0.25[(25 – 16.25)(30 – 23.75)] + 0.50[(15 – 16.25)(25 – 23.75)] + 0.25[(10 – 16.25) (15 – 23.75)] = 13.67 + (–0.78) + 13.67 = 26.56
请问老师,组合的方差为等于零,是代表什么深层含义?