NO.PZ2020011303000168
问题如下:
You can trade bonds lasting 0.5 years and one year that have coupons of 3% and 4%, respectively. If these bonds pay their coupons on a semi-annual basis, how could you use them to replicate the cash flows on a one-year bond paying a 5% coupon?
选项:
解释:
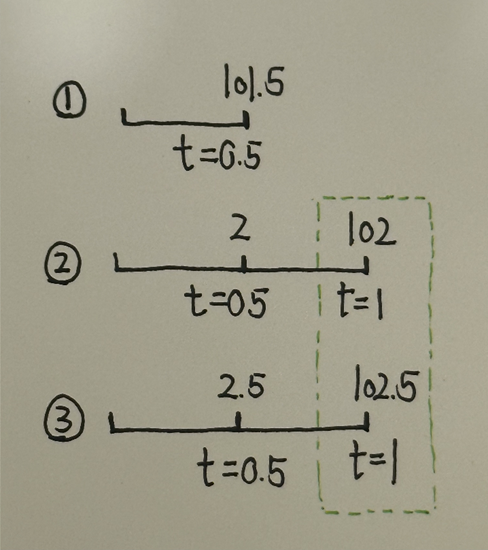
A one-year 5% coupon bond provides cash flows of 2.5 in six months and 102.5 in one year. We first replicate the one-year cash flow with:
102.5/102= 1.0049
of the one-year bond. This will provide a cash flow of 1.0049 × 2 = 2.0098 at the six month point. We therefore require an extra 0.4902 of cash flow at this point. This can be provided by:
0.4902/101.5= 0.00483
of the six-month bond.
题目问:0.5年期的债券coupon3%,1年期的债券coupon4%,这些债券半年付息一次,如何用这些债券复制一份现金流与一年期coupon5%半年付息一次的债券相同的债券?
一年期5%coupon半年付息一次的债券的现金流:CF0.5=2.5,CF1=102.5
首先用1年期4%coupon来进行复制,CF1=102,我们需要102.5/102=1.0049份4%coupon的债券,这个债券同时会提供CF0.5=2*1.0049=2.0098
我们还需要2.5-2.0098=0.4902的CF0.5,用0.5年期3%coupon的债券来复制,需要0.4902/101.5=0.00483份