问一道题：NO.PZ201712110200000304 第4小题 [ CFA II ]-有问必答-品职教育专注CFA ESG FRM CPA 考研等财经培训课程

问一道题：NO.PZ201712110200000304 第4小题 [ CFA II ]

* 问题详情，请查看题干

问题如下图：

选项：

解释：

请问这个no lockout period的callable bond的value是怎么算出来的？谢谢！

其实就是用每年的Forward rate把未来一年的现金流折现到每个节点，对比是否行权。

本题Exhibit 1就告诉了每一年的one-year frward rate。只不过不是二叉树形式。

这道题求含权债券价格和我们用二叉树求含权债券的做法是一模一样的。

只不过，我们二叉树里面见到的利率发展路径是这样的，是二叉树的。见红框：

而本题的利率发展路径是这样的：

无论是哪种路径，求含权债券的价格本质上都是一样的：

都是将下一年的总现金流（包括债券价格和Coupon）折现到上一个node，得到上一个node的债券价值，看看上一个node的债券价值是否会触发行权价。

如year 2的总现金流，折现到year 1，得到year 1的债券价值，再对比行权价。

如果触发就调整债券价值至行权价，然后加上该node的coupon组成该node的现金流，继续往上一个node折。

在二叉树里每一个树杈都是50%的权重；而本题的利率没有分叉，所以是100%的权重。

按题目给的信息：

Bond 4是一个maturity 3年，每年都可以用Par value行权的callable bond。

由于是每年都可以行权，所以每一年年末的时候（每一个Node），都要对比一下债券的价格是否会触发行权价。

需要用每一个node的One-year forward rate，将下一年的债券现金流（债券的价值加上coupon）折现到本期。得到本期的债券价格（价值）。

从第三年年末开始，将第三年的总现金流（债券到期面额，加上第三年的Coupon）折现到第二年末，得到第二年年末的债券价值；用到的折现率是第二年末的One-year forward rate：

发现第二年末的债券价格为100.1952大于行权价100，所以第二年末触发行权，将债券价格调整到100。

然后将第二年末调整后的债券价格100加上本年Coupon，组成第二年的总现金流，折现到第一年末，用到的折现率是第一年末开始的One-year forward rate：

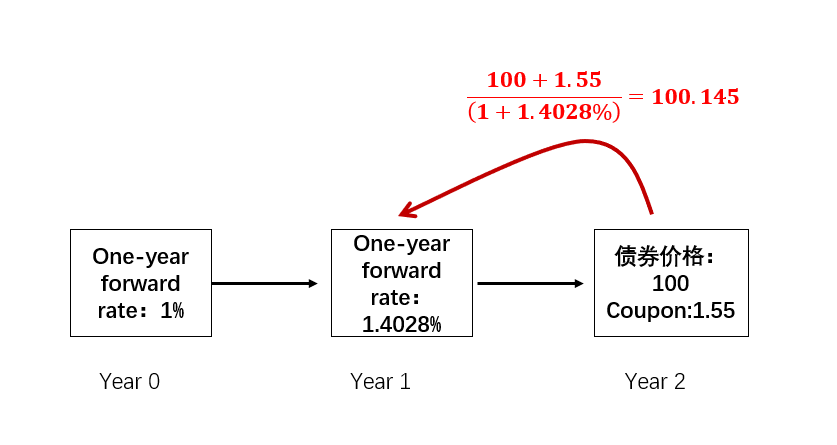
同理，callable bond，折现回来的价格发现触发行权价，将第一年末的债券价格调整到100，加上第一年的coupon，就能得到第一年的总现金流，把其往现在时刻折现，折现率是现在起的one-year forward rate：

所以，callable bond的现值是100.545

注意：有些题目会让求某个node的债券价值，所以把发生在该node之后的现金流折现到该node就好，得到的就是该node的债券价格，折现回来后不用加该node的Coupon。

本题并不是常见的二叉树，没有树杈，所以本题one-year forward rate的权重是100%，当出现二叉树时，每一个叉的权重是50%，所以折现回来求每个节点现值时要注意权重的影响。

问一道题：NO.PZ201712110200000304 第4小题 [ CFA II ]