这一段没有听懂，请老师讲解一下

嗨，努力学习的PZer你好：

这个问题从下面角度理解：

mad duration=∑(PVCFi/P)*t，代表的是现金流发生时间点的加权平均，权重是PVCFi/P，也就是该笔现金流现值占债券现值的比重，所以，简单的说，duration代表现金流的发生时间的平均值（当然，是加权平均）

convexity有两个计算公式

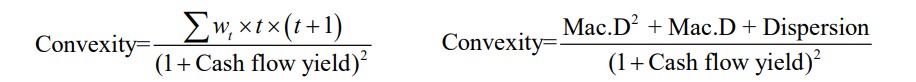
公式中的cash flow yield就是portfolio 的ytm，所以，如果从单只债券的角度说，cash flow yield就是Ytm

根据第一个公式，convexity是现金流发生时间的方差

根据第二个公式，convexity与现金流的离散程度（dispersion）成正比，可以用convexity代表现金流的离散程度，

也就是说，现金流越离散（越分散），duration相同时，convexity越大。

这两个公式不会考察计算

但是这个结论要记住，就是conveixty代表现金流离散程度，duration相同时，现金流越分散，convexity越大。

至于“duration相同，CF越分散说明前面的现金流越多，maturity越长”

这句话可以用相同duration的零息债和付息债比较来佐证。

零息债的剩余到期日等于duration

付息债的剩余到期日大于duration（这个可以随便用mac duration的计算公式举例证明）

所以，如果一只零息债的duration等于一只付息债的duration，那么这只付息债的期限肯定是要长期与零息债的。

举例，一只付息债，coupon=3，期限是2年，ytm是1.5%

P=102.93

PVCF1=3/(1+1.5%）=2.96

PVCF2=103/(1+1.5%)^2=99.98

mac duration=2.96/102.93+99.98*2/102.93=1.94

2年期的付息债的久期是1.94，那么可以找一只剩余期限1.94年的零息债，它的久期也是1.94

两只债的久期都是1.94，但付息债的剩余期限是2年大于零息债的剩余期限1.94年。

零息债只有一笔现金流，付息债有两笔现金流，所以现金流更分散。

所以，duration，CF越分散，maturity越长。

----------------------------------------------
虽然现在很辛苦，但努力过的感觉真的很好，加油！