NO.PZ2022122801000046
问题如下:
Remington and Montgomery
discuss Isabelle Sebastian. During a recent conversation, Sebastian, a
long-term client with a $2,900,000 investment portfolio, reminded Remington
that she will soon turn age 65 and wants to update her investment goals as
follows:
Goal 1: Over the next 20 years, she needs to maintain
her living expenditures, which are currently $120,000 per year (90% probability
of success). Inflation is expected to average 2.5% annually over the time
horizon, and withdrawals take place at the beginning of the year, starting
immediately.
Goal 2: In 10 years, she wants to donate $1,500,000 in nominal terms
to a charitable foundation (85% probability of success).
Exhibit 2 provides
the details of the two sub-portfolios, including Sebastian’s allocation to the
sub-portfolios and the probabilities that they will exceed the expected minimum
return.
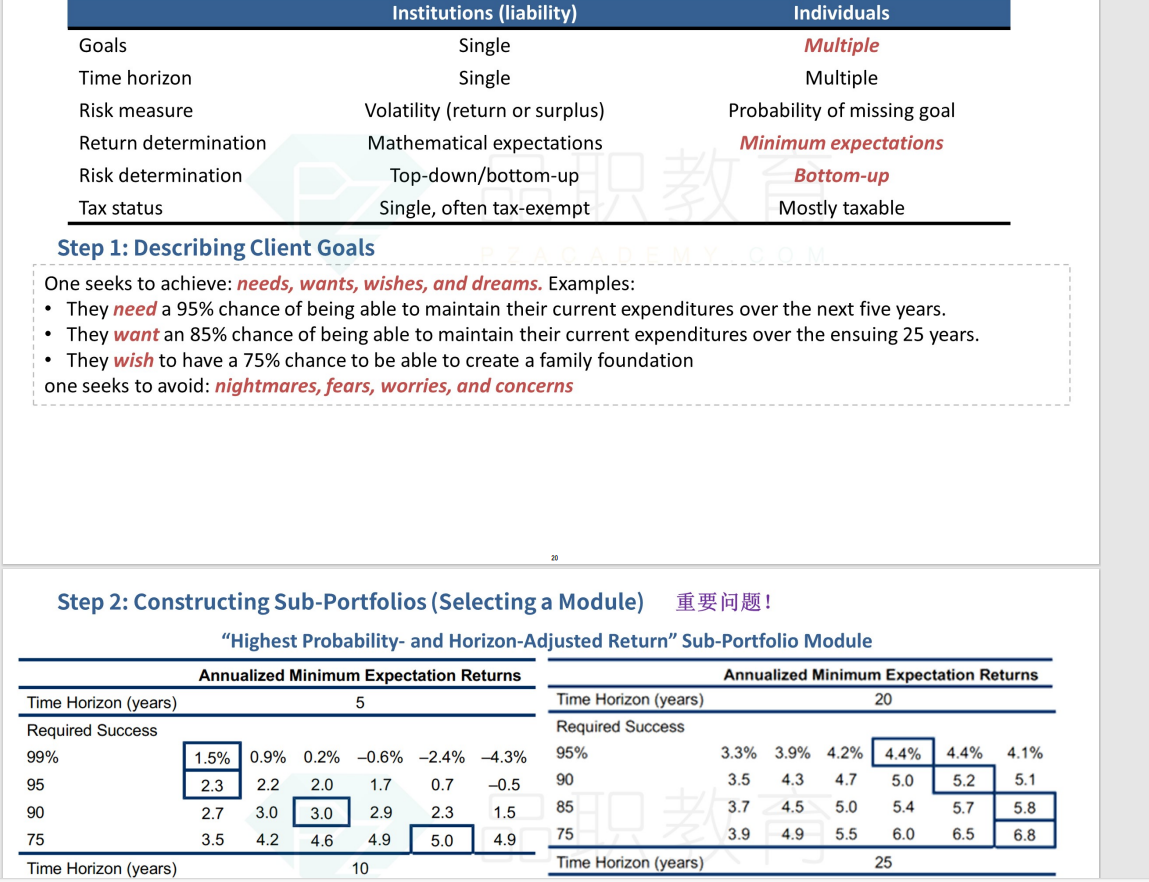
Exhibit 2 Investment Sub-Portfolios & Minimum Expected Return
for Success Rate


Assume 0% correlation between
the time horizon portfolios.
Using Exhibit 2, which of the sub-portfolio allocations is most likely to meet both of Sebastian’s goals?
选项:
A.The current sub-portfolio allocation
A 43% allocation to sub-portfolio BY and a 57% allocation to sub-portfolio CZ
A 37% allocation to sub-portfolio BY and a 63% allocation to sub-portfolio CZ
解释:
Sebastian needs to adjust the sub-portfolio allocation to achieve her goals. By adjusting the allocations to 37%×$2,900,000=$1,073,000 in BY and 63%×$2,900,000 = $1,827,000 in CZ, she will be able to achieve both of her goals based on the confidence intervals.
Goal 1: Sebastian needs to maintain her current living expenditure of $120,000 per year over 20 years with a 90% probability of success. Inflation is expected to average 2.5% annually over the time horizon.
Sub-portfolio CZ should be selected because it has a higher expected return (5.70%) at the 90% probability for the 20-year horizon. Although sub-portfolio CZ has an expected annual return of 7.10%, based on the 90% probability of success requirement, the discount factor is 5.70%.
Goal 1: k = 5.70%; g = 2.50%.
Determine the inflation-adjusted annual cash flow generated by sub-portfolio CZ:
Goal 2: Sebastian wants to contribute $1,500,000 to a charitable foundation in 10 years with an 85% probability of success.
Sub-portfolio BY should be selected because it has a higher expected return (3.60%) at the 85% probability for the 10-year horizon. Although sub-portfolio BY has an expected annual return of 5.70%, based on the 85% probability of success requirement, the discount factor is 3.60%.
Goal 2: k = 3.60%.
Determine the amount needed today in sub-portfolio BY:
RT