老师您好,
有个Equity比较细节的问题想请教您:Module 1中的2.3和2.4这两道题非常相似,但是在折现的时候2.3的现货价格和红利折了两次,而2.4只折了一次,不知道这其中的缘由是什么。我看了很久也没能看出来他们的区别,所以想请教一下您

李坏_品职助教 · 2023年10月22日
嗨,从没放弃的小努力你好:
2.3题:远期合约的期限是9个月,合约的到期日是t=0.75。现在是已经过了3个月了,现在t = 0.25。
在t=0.5的时候会发放一笔现金红利。这个现金红利是预计在未来t=0.5发放的,所以先折现到0.25时刻,再用0.25时刻的股票价格245减去他,然后复利到0.75的合约到期日。
所以t=0.25时刻的远期价格F0.25 = (245-1.5/(1+0.00325)^0.25) * 1.00325^(0.75-0.25)。
这个F0.25指的是在0.25时刻计算出来的理论上在0.75到期日的时候的远期价格,但是0时刻已经确定了一个远期价格是F0,现在要计算这两个的差值,差值体现出来在0.75时刻的合约价值。最后进行二次折现,0.75折到0.25时刻。Value = (F0.25-F0)/ (1+0.00325)^(0.75-0.25)
2.4题:股票远期的期限是250天,一共会发放3笔红利,分别都折现到0时刻。
计算F0 = (股票0时刻价格 - 3笔红利的现值之和)*(1+rf)^(250/360)。
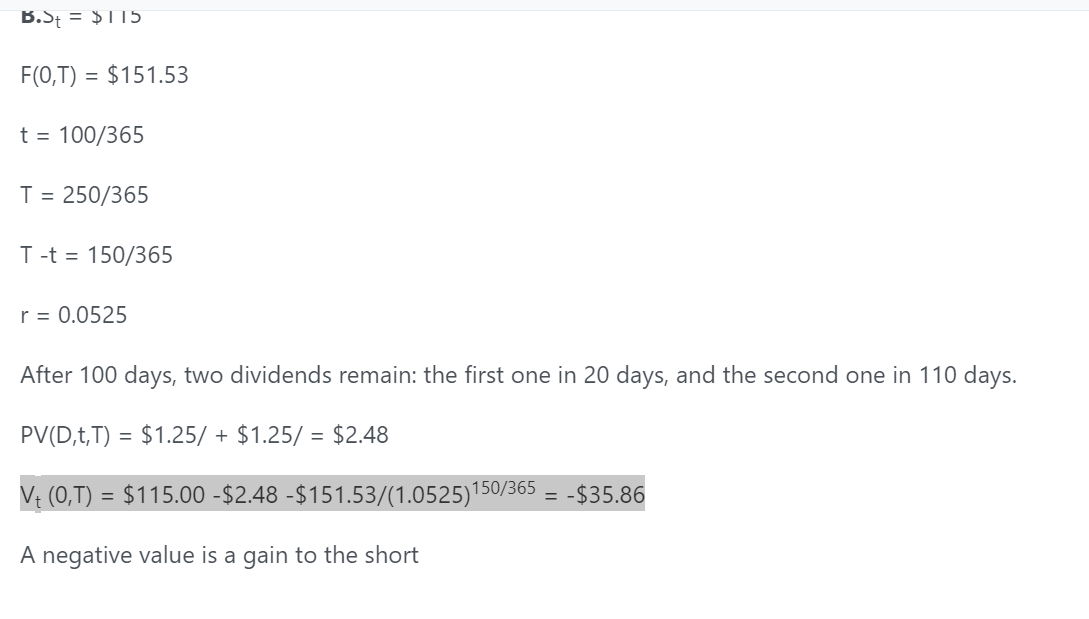
然后第二小问说已经过去了100天,F100/365 = (115-2.48)*(1+rf)^(150/365).
参照2.3的算法,那就应该是F100/365 - F0,然后从250天折现到100天。
在100天时刻的合约value = (F100/365 - F0)/(1+rf)^(150/365) = [(115-2.48)*1.00525^(150/365) - 151.53)]/ 1.00525^(150/365)
= 115-2.48 - 151.53/1.00525^(150/365)。
我用2.3那种折现两次的方法,算2.4得到了正确答案。所以你会发现这两道题是完全等价的。
----------------------------------------------
就算太阳没有迎着我们而来,我们正在朝着它而去,加油!
Haosai · 2023年10月23日
感谢老师这么细致地回答!完全明白了