NO.PZ2019010402000021
问题如下:
A manager plans to estimate the value of American-style put option by using two-period binomial model. The current stock price is $32, and exercise price of put option is $32.The up factor is 1.12, and the down factor is 0.92. The risk-free rate is 5%. The value of this put option is:
选项:
A.
0.5461
B.
0.8533
C.
1.0432
解释:
B is correct.
考点:二叉树求value
解析:
画二叉树
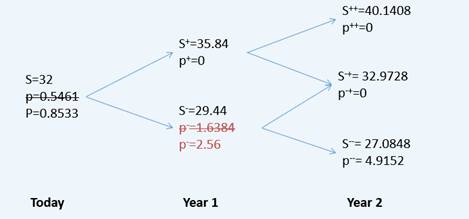
这一题是美式期权,在t=1时执行,put的价值更高(=32-29.44=2.56),所以投资者会选择提前执行。此时
1.p++、p+-和p--的公式是什么?
2.请在纸上写一下完整过程,越详细越好。



