嗨,爱思考的PZer你好:
你提到的问题涉及到现代投资组合理论和多因子模型之间的一些概念。首先,我们解释一下背景,然后再回答你的问题。
- 现代投资组合理论 (Modern Portfolio Theory, MPT): 这是一个描述资产收益、风险和相关性如何影响组合总体风险和回报的理论。在这个理论中,资产之间的相关性(通常表示为ρ或rou)是核心的概念,因为通过组合低相关性或负相关性的资产,可以有效地降低组合的整体风险,这就是所谓的diversification或分散化。
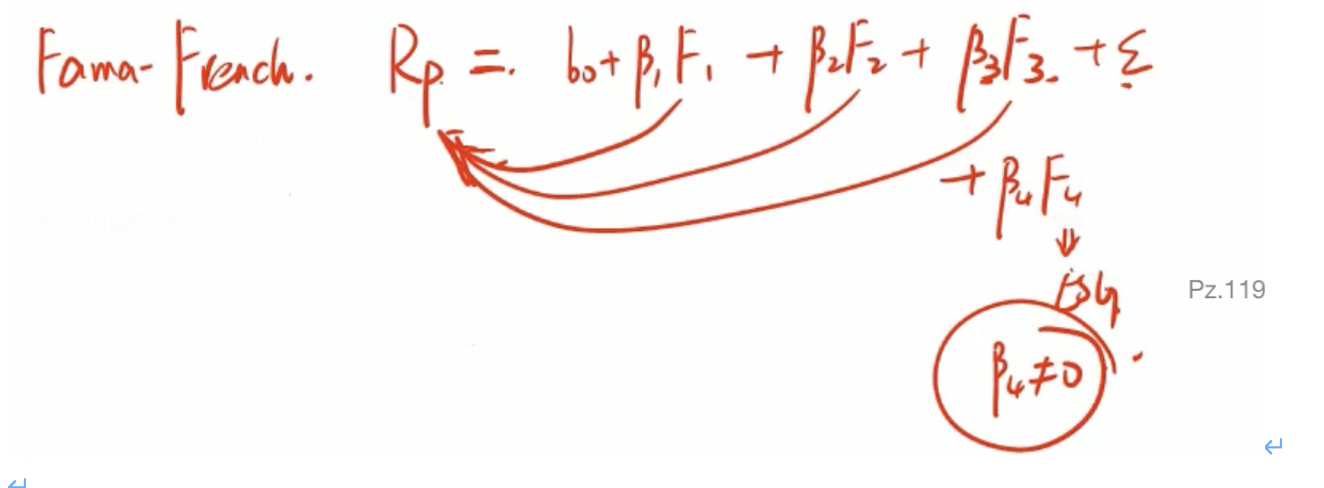
- 多因子模型 (Factor Models): 这是一个尝试解释资产收益的模型,通常使用多个“因子”或变量。这些因子可能是宏观经济变量(如利率、通货膨胀率等)或是投资风格相关的因子(如市值、账面市值比、动量等)。
当选择模型的因子时,研究者通常会考虑到这些因子之间的相关性,并努力选择那些相对独立的因子,以确保模型的解释性和稳定性。
为了解决这一问题,研究者和实践者通常采用以下方法来剔除或减少因子间的相关性:
- 因子选择:在模型的设计阶段,可以选择那些相对独立的因子,即那些与其他因子相关性低的因子。这通常是通过相关性分析和领域知识来完成的。
- 因子正交化:正交化是一个数学过程,旨在使两个或多个变量变得相互独立。在多因子模型中,如果我们认为两个因子可能存在相关性,我们可以使用数学技术(如格拉姆-施密特正交化过程)来使它们正交,从而消除它们之间的相关性。
- 主成分分析 (PCA):PCA是一个常用的技术,可以从原始的、可能相关的因子中提取出一组新的、互不相关的主成分。这些主成分可以作为新的因子用于模型。
- 正则化方法:例如L1正则化(Lasso)或L2正则化(Ridge)。这些方法可以在估计模型时加入一个惩罚项,以处理因子之间的共线性,并且可以帮助选择最重要的因子。
- 组合因子:如果两个因子高度相关,它们可能都是某个潜在变量的表现。在这种情况下,可以考虑将这两个因子合并为一个单一的组合因子。
- 差异化处理:例如,如果两个经济指标高度相关,可以考虑使用这两个因子的差值或比率作为新的因子,以消除它们之间的线性相关性。
总的来说,处理因子之间的相关性是多因子模型设计和估计过程中的一个关键步骤。在实际应用中,研究者和实践者需要结合统计方法和业务知识,仔细选择和处理因子,以确保模型的稳定性和解释力。
----------------------------------------------
就算太阳没有迎着我们而来,我们正在朝着它而去,加油!