NO.PZ2022062760000001
问题如下:
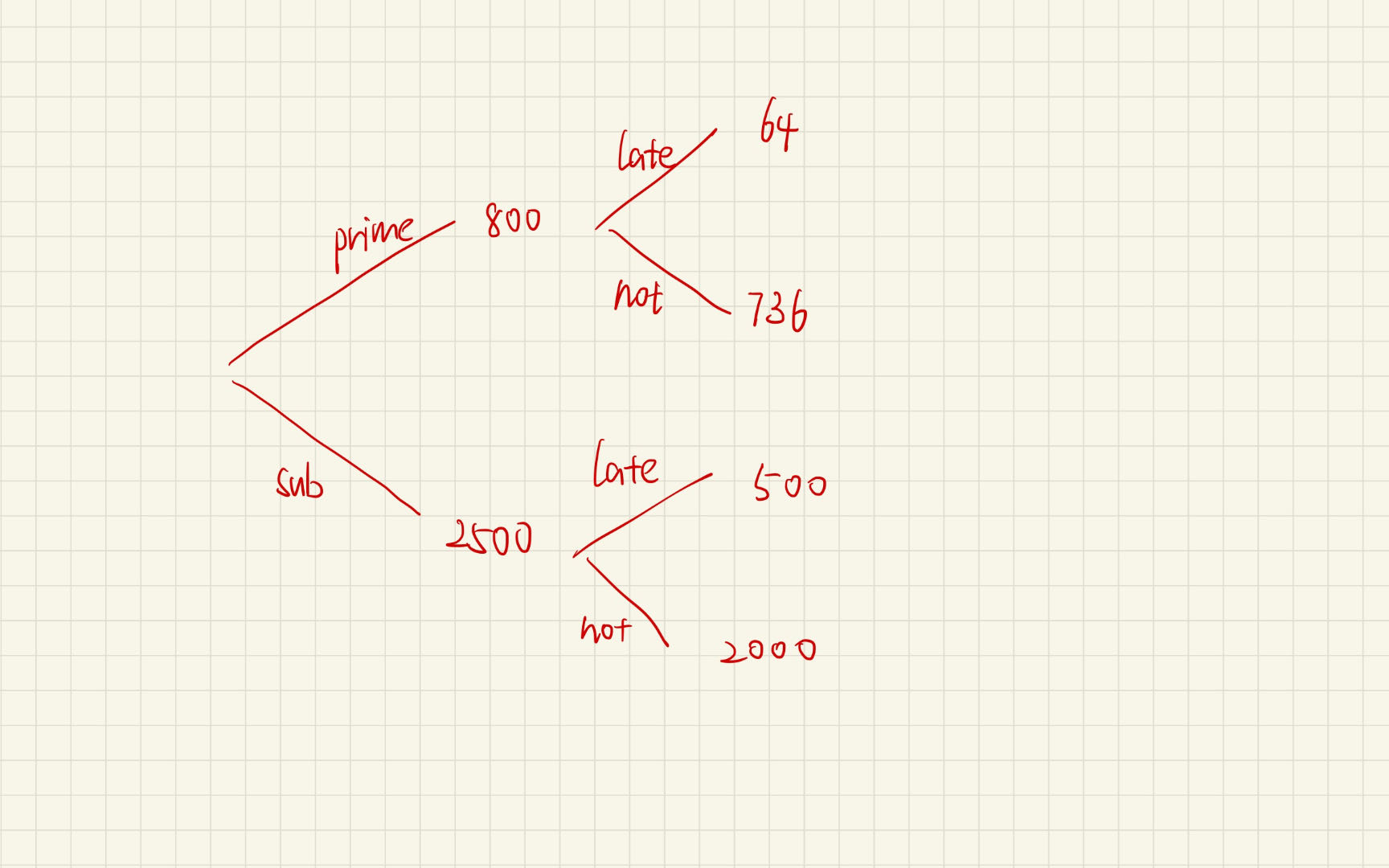
An analyst is examining a portfolio that consists of 2,500 subprime mortgages and 800 prime mortgages. Of
the subprime mortgages, 500 are late on their payments. Of the prime mortgages, 64 are late on their
payments. If the analyst randomly selects a mortgage from the portfolio and it is currently late on its
payments, what is the probability that it is a subprime mortgage?
选项:
A.
60%
B.
67%
C.
75%
D.
89%
解释:
中文解析:
求条件概率:
P(Mortgage is late) = (500+64)/(2500+800) = 17.1%
P(Subprime mortgage and late) = 500/3300 = 15.2%
P(Subprime mortgage | Mortgage is late) = P(Subprime mortgage and late)/P(Mortgage is late) = 15.2% / 17.1% = 0.89 = 89%
In order to solve this conditional probability question, first calculate the probability that any one mortgage in the portfolio is late.
This is: P(Mortgage is late) = (500+64)/(2500+800) = 17.1%.
Next, use the conditional probability relationship as follows: P(Subprime mortgage | Mortgage is late) = P(Subprime mortgage and late)/P(Mortgage is late).
Since P(Subprime mortgage and late) = 500/3300 = 15.2%, then
P(Subprime mortgage | Mortgage is late) = 15.2% / 17.1% = 0.89 = 89%.
Hence the probability that a random late mortgage selected from this portfolio turns out
to be subprime is 89%.
图中标注比例还是直接带入数字会方便一点?