有点儿混了,convexity类似于option,都对投资者有利,涨多跌少,那为什么delta是小于1的?
delta=0.3就是股价长1,option长0.3,这不是长得少么
我觉得是我偷换概念了,请助教轻拍。谢谢。
发亮_品职助教 · 2018年05月20日
Duration是债券价格对收益率的一阶导,对应在option里,一阶导是delta,即Option价格对标的物价格一阶导;
Convexity是债券价格对收益率的二阶导,对应在option里,二阶导是gamma,即option价格对标的物价格的二阶导。
涨多跌少的性质,是由债券的Convexity和option的gamma带来的。
如下图所示,蓝色和红色是两个Bond,蓝色的Convexity更大。
绿色虚线表示债券价格和YTM的线性关系,即duration衡量。
当利率降低时,duration衡量的是债券价格的线性变化。
但是债券的价格的实际涨幅由曲线所示,红色和蓝色的债券涨幅都比单纯考虑Duration线性关系的涨幅更大;
反映在图里,就是曲线都比直线涨的高。同理收益率上升,价格下跌时,曲线又在直线上面。
这样就是我们说的涨多跌少的性质,这是由Convexity带来的。
同时蓝色的Convexity较大,所以涨幅又相比红色更大。

当考虑Option时,
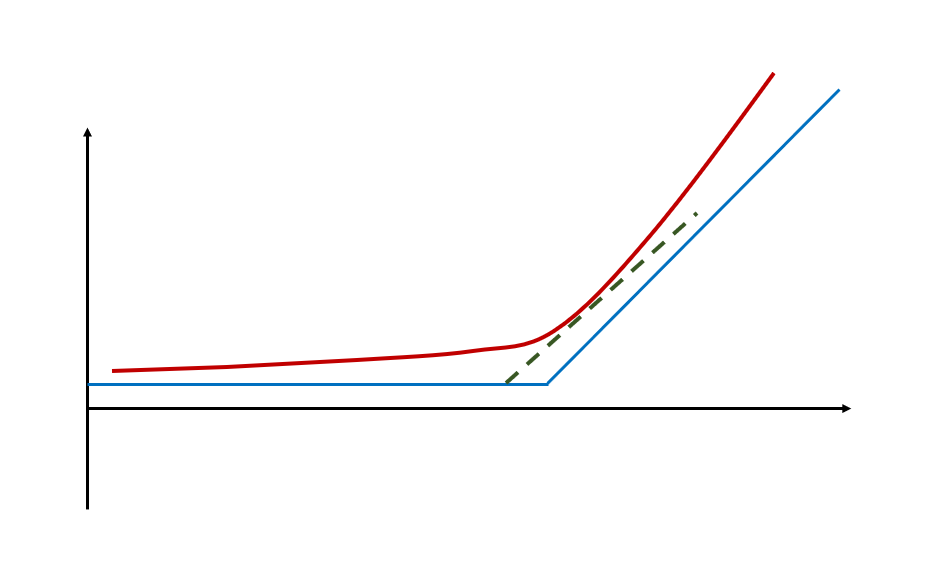
绿色虚线表示是用delta衡量的标的物价格和option价格之间的线性关系。
当标的物价格上升时,Option的实际价格上升幅度大于仅仅用Delta衡量的结果。
所以期权同样具有涨多跌少的性质,这也类似于债券里的Convexity属性。
为什么期权具有Convexity特性?这是由于Gamma的存在。
Gamma永远是非负数;以Call option为例,当标的物价格上升时,用delta衡量Call option价格上升,但是Gamma的存在使得call option价值进一步上升。这就是涨多。同理跌少,也是有gamma带来的。
所以当预测收益率波动性加大时,在Bond portfolio的duration和convexity即定的情况下,通过Long option增加组合的Convexity。无论收益率上升或者下跌,Convexity更大实现portfolio的涨多跌少(相比原来的bond portfolio)。
当然,option的头寸也会进一步改变bond portfolio的duration,原版书在这里假设我们用option调整Convexity时,已经考虑过了option对duration的影响。
所以在yield curve strategy,增加减少convexity时,可以通过option的头寸来实现。