为何用二叉树模型估值时，interest rate volatility 不会影响option-free bond的价格？

感谢助教大大的详尽回复！我一开始推导问题中的等式，也用到了middle rate≈f这个条件，但是在最后整理提问的过程中，把这个条件去掉了，因为我感觉这是建立二叉树过程中，calibrate这一步骤的结果，而非前提假设。而您给出的证明似乎也正是对calibrate的验证？我又重新整理了一个推导过程，在这个过程中，假设了一个更加一般的middle rate（m），不论其是否等于f，都能得到V0是sigma的减函数这一结论。其实，即使以您给出的例子，对于一个确定的implied f，代入一个更大的sigma，V0也是减小的。 因为没有其他合适途径反馈，我擅自在自己问题下新建了一个答案，把过程贴上去了，请您指点一下！感谢！

Calibration推出来的二叉树，只要让其满足benchmark bond的折现求和值等于市场价格就好了。剩下其他的Bond，在这个二叉树的基础上加上Spread就是对应的二叉树。

比如，再求Callable bond的价值时，是在benchmark二叉树基础上加上了OAS，然后折现。

原因就是benchmark的折现率，也是其他债券折现率的一部分。

关于二叉树，还有一个假设：

二叉树里每一期的Middle rate大体上等于那一期的implied forward rate。

可以简单的想一下这个道理：

以1期二叉树为例，现在时刻有两种forward rate，RL和RH，各有50%的权重。

第一年的Spot rate等于implied forward rate，RL与RH之间差两个标准差，其中RH比第一年的spot rate（implied forward rate）高、RL比第一年的spot rate（implied forward rate）低；考虑50%的权重之后又让二叉树折现值等于用implied forward rate折现值；所以推断RH比implied forward rate高一个sigma，RL比implied forward rate低一个sigma。

再把二叉树推广到2期，由于第一期的up和down是围绕着implied forward rate展开的；为了让2期的二叉树折现出来的价值等于现值，那么第二期的各个分叉仍然是围绕着对应的implied forward rate。

下面用一个实际例子，来证明middle rate等于implied forward rate。

在构建二叉树时，我们从par rate/spot rate/implied forward rate开始，注意无论用哪个都可以，因为三者知道其一就可以互相推导。

假设，在二叉树模型中，我们的standard deviation是15%；我们知道1年期国债的par rate是10%。

那这样的话，一年期的Spot rate = implied forward rate = 10%

将二叉树从0期推到1期，知道H和L的差距是2个standard deviation。

此时我们找到一个2年期国债，假设par rate是15%，根据二叉树折现，有以下：

整理一下将R1H替换成R1L有：

得到：

R1L=0.181

则，可求：R1H=0.245

从1年期的par rate我们知道一年期的spot rate=10%，有2年期的par rate=15%，根据bootstrapping可以求2年期的spot rate：

求得2年期的Spot rate为15.39%

这样implied forward rate可求：

则f1,1=21.05%。

我们分别用R1H除以f11，用f11除以R1L：

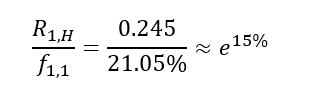
发现up和down是围绕着implied forward rate展开的。所以二叉树本身蕴含的信息仍是当前市场的spot rate/implied forward rate的信息。结合了利率的波动率sigma，在当前implied forward rate的基础上，衍生出了各种路径，二叉树的骨干仍是Implied forward rate，只要implied forward rate不变，不论Sigma的增大或者减少，折现出来的值仍不变，只不过sigma增大时，二叉树的树杈更分散。

二叉树的各节点的middle rate近似等于implied forward rate。

消除掉sigma变化影响的原因是，分叉forward rate围绕着implied forward rate，sigma虽然变化，但是implied forward rate没变，所以你上面的推导没有用到这点，另外这个围绕关系也是一个近似相等。