NO.PZ2020011303000145
问题如下:
The 5 and 95 percentiles of a lognormal loss distribution are 50 and 200. What is the 99.7 percentile of the distribution?
选项:
解释:
The 5 and 95-percentiles of the logarithm of the loss are ln(50) and ln(200), (i.e., 3.912 and 5.298). The logarithm of the loss has a mean of (3.912 + 5.298)/2 = 4.605 and a standard deviation of (5.298 – 4.605)/1.645 = 0.421. The 99.7-percentile of the logarithm of the loss is 4.605 + N-1(0.997) × 0.421 = 5.763. The 99.7-percentile of the loss is therefore e5.763 =318.3
题目问:损失的对数正态分布5%和95%的分位点对应的是50和200,求99.7%的损失是多少?
对于对数正态分布,5%和95%的损失为ln(50)和ln(200),也就是3.912和5.298,均值为(3.912+5.298)/2=4.605,标准差为 (5.298 – 4.605)/1.645 = 0.421,ps.1.645是95%的z值。
99.7% 分位点的值是4.605+ N-1(0.997) *0.421=5.763,损失=e^5.763=318.3。
1.standard deviation 为什么这么算? (5.298 – 4.605)/1.645 = 0.421
我用计算器算出来的是0.693147,为什么不这么计算标准差?
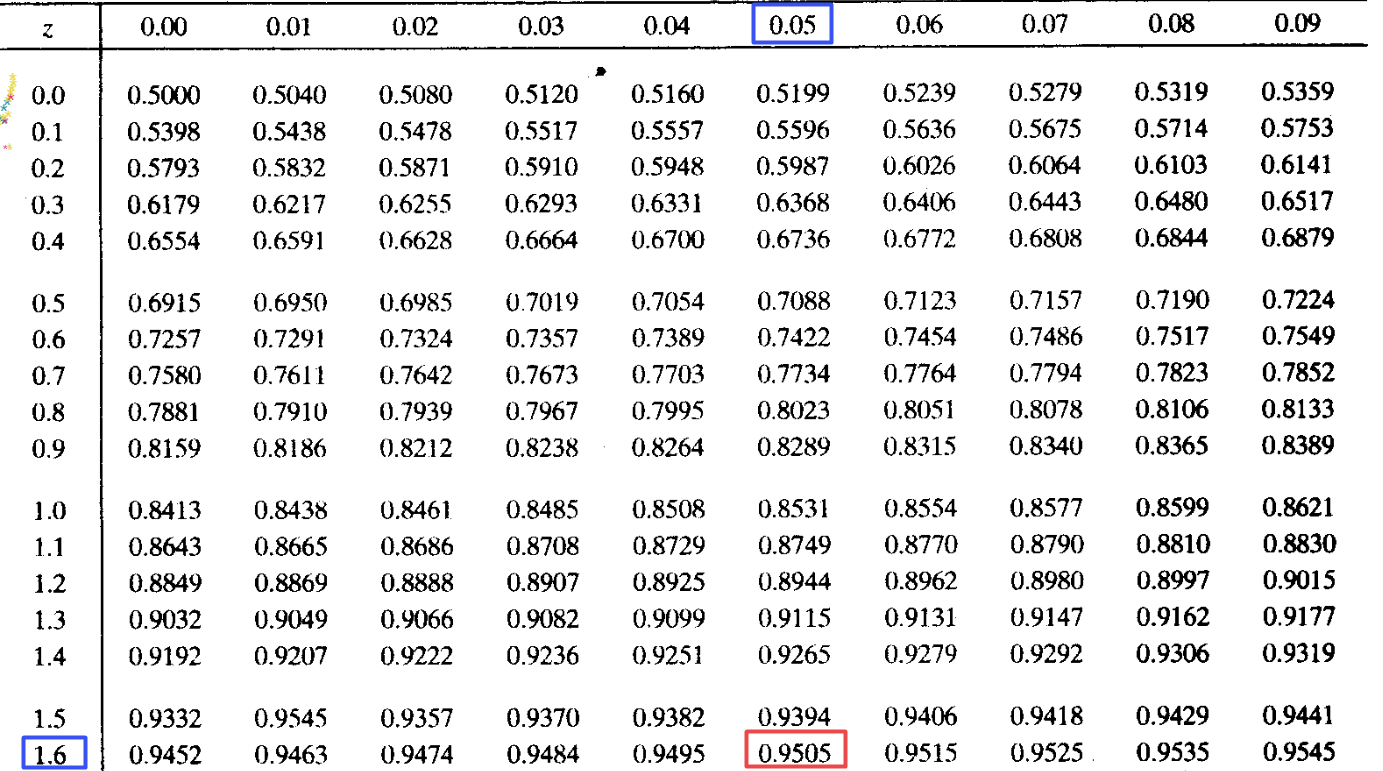
2.1.645是怎么得出的?如果是查表,具体怎么查?
谢谢。