开发者:上海品职教育科技有限公司 隐私政策详情

应用版本:4.2.11(IOS)｜3.2.5(安卓)APP下载

返回

Cooljas · 2022年05月17日

请教下 用这三个概率怎么查表呀？

  1. FRM I
  2. Quantitative

NO.PZ2020010303000011

问题如下：

If the return on a stock, R, is normally distributed with a daily mean of 8%/252 and a daily variance of (20%)2/252(20\%)^2/252, find the values where

a. Pr(R < r) = .001

b. Pr(R < r) = .01

c. Pr(R < r) = .05

选项：

解释：

a. The mean is 0.031% per day and the variance is 1.58 per day (so that the standard deviation is 1.26% per day). To find these values, we transform the variable to be standard normal, so that

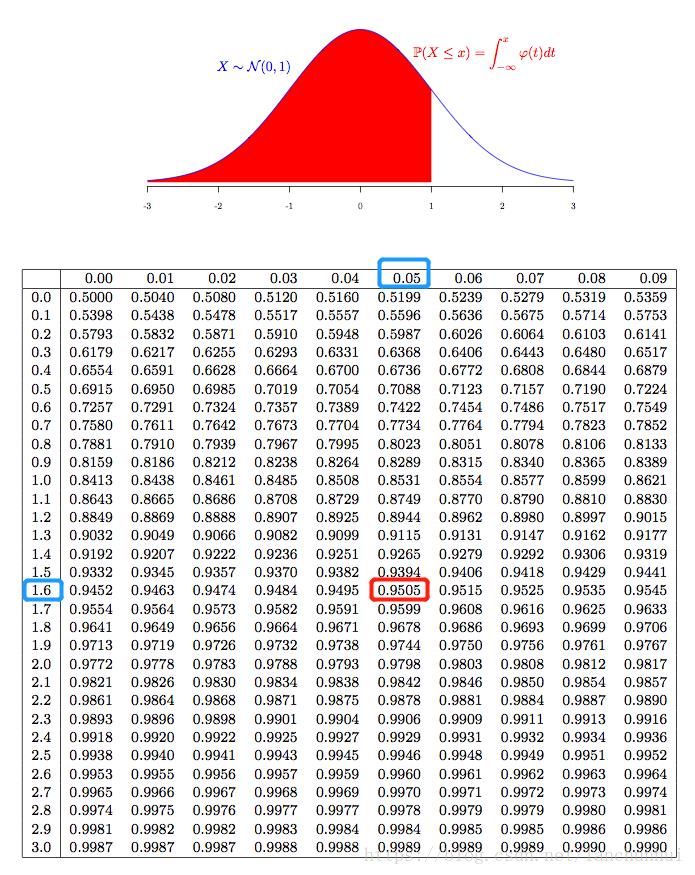
Pr(R<r)=.001=Pr(Z<r−μσ)=.001 Pr(R < r) = .001 = Pr(Z<\frac{r-\mu}{\sigma})= .001

The value for the standard normal is -3.09

(NORM.S.INV(0.001) in Excel) so that −3.09∗σ+μ=−3.86%-3.09 * \sigma + \mu = -3.86\%.

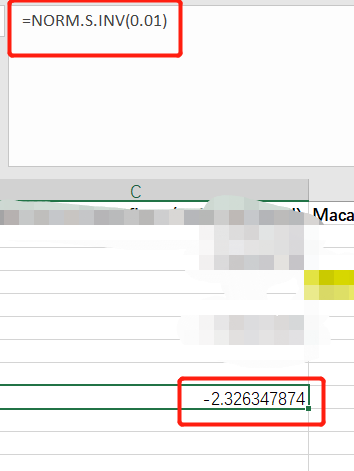
b. The same idea an be used here where z = -2.32 so that Pr(Z < z) = .01. Transforming this value, r=−2.32∗σ+μ=−2.89%r = -2.32 * \sigma + \mu = -2.89\%.

c. Here the value of z is -1.645 so that r=−1.645∗σ+μ=−2.04%r = -1.645 * \sigma + \mu = -2.04\%.

These are all common VaR quan-tiles and suggest that there is a 5% chance that the return would be less than -2.04% on any given day, a 1% change that it would be less than -2.89%, and a one in 1,000 chance that the return would be less than -3.86%, if returns were normally distributed.



添加评论
2 个答案

李坏_品职助教 · 2022年05月18日

嗨，努力学习的PZer你好：


精确答案可以用excel的红框里面的公式得到：

所以四舍五入结果是2.33，答案这里不是很精确

----------------------------------------------
加油吧，让我们一起遇见更好的自己！

李坏_品职助教 · 2022年05月17日

嗨，努力学习的PZer你好：


0.05是α值，在标准正态分布表里，我们要去找最接近1-α的那个数字对应的x值。

在标准正态分布表里面第一列是x的整数位和小数点后第一位数字，第一行是x的小数点后第二位数字，所以你会发现x=1.65的时候，对应的数字是0.9505，是最接近0.95的，所以α=0.05的时候，对应的标准差倍数就是1.65倍了。

----------------------------------------------
努力的时光都是限量版，加油！

Cooljas · 2022年05月18日

当α是0.01的时候，查表得z=2.33的概率明明更接近于0.99，为啥答案中取的z=2.32呢？

  • 2

    回答

  • 0

    关注

  • 474

    浏览
相关问题

NO.PZ2020010303000011问题如下 If the return on a stock, R, is normally stributewith a ily meof 8%/252 ana ily varianof (20%)2/252(20\%)^2/252(20%)2/252, finthe values where Pr(R r) = .001Pr(R r) = .01Pr(R r) = .05 The meis 0.031% per y anthe varianis 1.58 per y (so ththe stanrviation is 1.26% per y). To finthese values, we transform the variable to stanrnormal, so thatPr(R r)=.001=Pr(Z r−μσ)=.001 Pr(R r) = .001 = Pr(Z \frac{r-\mu}{\sigma})= .001 Pr(R r)=.001=Pr(Z σr−μ​)=.001The value for the stanrnormis -3.09(NORM.S.INV(0.001) in Excel) so th−3.09∗σ+μ=−3.86%-3.09 * \sigma + \mu = -3.86\%−3.09∗σ+μ=−3.86%.The same ia usehere where z = -2.33 so thPr(Z z) = .01. Transforming this value, r=−2.33∗σ+μ=−2.89%r = -2.33 * \sigma + \mu = -2.89\%r=−2.33∗σ+μ=−2.89%.Here the value of z is -1.645 so thr=−1.645∗σ+μ=−2.04%r = -1.645 * \sigma + \mu = -2.04\%r=−1.645∗σ+μ=−2.04%.These are all common Vquan-tiles ansuggest ththere is a 5% chanththe return woulless th-2.04% on any given y, a 1% change thit woulless th-2.89%, ana one in 1,000 chanththe return woulless th-3.86%, if returns were normally stribute 老师好，方差是用20%^2/252吗？这样算，得出的是方差是0.0158%，而不是1.58%。另外，20%^2大于252，能直接用20%^2除以252吗？

2024-05-27 14:22 2 · 回答

NO.PZ2020010303000011 问题如下 If the return on a stock, R, is normally stributewith a ily meof 8%/252 ana ily varianof (20%)2/252(20\%)^2/252(20%)2/252, finthe values where Pr(R r) = .001Pr(R r) = .01Pr(R r) = .05 The meis 0.031% per y anthe varianis 1.58 per y (so ththe stanrviation is 1.26% per y). To finthese values, we transform the variable to stanrnormal, so thatPr(R r)=.001=Pr(Z r−μσ)=.001 Pr(R r) = .001 = Pr(Z \frac{r-\mu}{\sigma})= .001 Pr(R r)=.001=Pr(Z σr−μ​)=.001The value for the stanrnormis -3.09(NORM.S.INV(0.001) in Excel) so th−3.09∗σ+μ=−3.86%-3.09 * \sigma + \mu = -3.86\%−3.09∗σ+μ=−3.86%.The same ia usehere where z = -2.33 so thPr(Z z) = .01. Transforming this value, r=−2.33∗σ+μ=−2.89%r = -2.33 * \sigma + \mu = -2.89\%r=−2.33∗σ+μ=−2.89%.Here the value of z is -1.645 so thr=−1.645∗σ+μ=−2.04%r = -1.645 * \sigma + \mu = -2.04\%r=−1.645∗σ+μ=−2.04%.These are all common Vquan-tiles ansuggest ththere is a 5% chanththe return woulless th-2.04% on any given y, a 1% change thit woulless th-2.89%, ana one in 1,000 chanththe return woulless th-3.86%, if returns were normally stribute 请问这是已知概率，反求z的取值吗？查表方式可以计算？

2024-01-15 00:20 4 · 回答

老师，这道题你了，但是我没有理解，请详细下这套题的分析过程。

2020-02-22 18:13 1 · 回答

a ily varianof (20%)²>252 怎么推出“the varianis 1.58 per y (so ththe stanrviation is 1.26% per y)”？

2020-02-15 20:01 1 · 回答