NO.PZ2021062201000005
问题如下:
An analyst estimates that 20% of high-risk bonds will fail (go bankrupt). If she applies a bankruptcy prediction model, she finds that 70% of the bonds will receive a "good" rating, implying that they are less likely to fail. Of the bonds that failed, only 50% had a "good" rating.
Use Bayes' formula to predict the probability of failure given a "good"rating. (Hint, let P(A) be the probability of failure, P(B) be the probability of a "good" rating, P(B | A) be the likelihood of a "good" rating given failure, and P(A | B) be the likelihood of failure given a "good" rating.)
选项:
A.5.7%
B.14.3%
C.28.6%
解释:
B is correct. With Bayes' formula, the probability of failure given a "good"rating is:
where
P(A) = 0.20 = probability of failure
P(B) =0.70 = probability of a "good" rating
P(B | A) =0.50 = probability of a "good" rating given failure
With these estimates, the probability of failure given a "good" rating is:
If the analyst uses the bankruptcy prediction model as a guide, the probability of failure declines from 20% to 14.3%.
知识点:Probability Concepts-Bayes' Formula
按照老师课堂的讲解画图得出的答案不应该是15%吗?如下图
- CFA I
- Quantitative
NO.PZ2021062201000005
问题如下:
An analyst estimates that 20% of high-risk bonds will fail (go bankrupt). If she applies a bankruptcy prediction model, she finds that 70% of the bonds will receive a "good" rating, implying that they are less likely to fail. Of the bonds that failed, only 50% had a "good" rating.
Use Bayes' formula to predict the probability of failure given a "good"rating. (Hint, let P(A) be the probability of failure, P(B) be the probability of a "good" rating, P(B | A) be the likelihood of a "good" rating given failure, and P(A | B) be the likelihood of failure given a "good" rating.)
选项:
A.
5.7%
B.
14.3%
C.
28.6%
解释:
B is correct. With Bayes' formula, the probability of failure given a "good"rating is:
P(A|B) = \frac{{P(B|A)}}{{P(B)}}P(A)P(A∣B)=P(B)P(B∣A)P(A)
where
P(A) = 0.20 = probability of failure
P(B) =0.70 = probability of a "good" rating
P(B | A) =0.50 = probability of a "good" rating given failure
With these estimates, the probability of failure given a "good" rating is:
P(A|B) = \frac{{P(B|A)}}{{P(B)}}P(A) = \frac{{0.5}}{{0.7}} \times 0.20 = 0.143P(A∣B)=P(B)P(B∣A)P(A)=0.70.5×0.20=0.143
If the analyst uses the bankruptcy prediction model as a guide, the probability of failure declines from 20% to 14.3%.
知识点:Probability Concepts-Bayes' Formula
添加评论
- 0 0
1 个答案
已采纳答案
星星_品职助教 · 9 个月前
同学你好,
问题在这个地方。
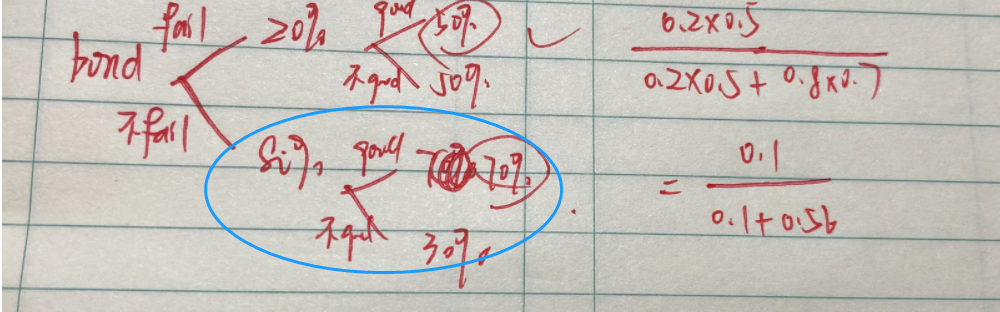
根据题干,“.... she finds that 70% of the bonds will receive a "good" rating”,可以看出这个70%是非条件概率。并不是在bond“bu fail”的条件下才有70%的可能。
所以,这道题和上课讲的题型不同,并不是用画图的方式来解的。
-----------
比较一下这道题目和此前画图解的贝叶斯公式题目的区别。可以看出这道题给的是两个非条件概率,例如本题就是20% will fail 和70% receive a "good" rating。
而普遍的贝叶斯公式的题型(可以参照基础班讲义上的机器诊断和有病的那道题)是只给一个非条件概率,这个画在图像的第一支;然后再给一个条件概率,画在图像的第二支。这种题型才是用画图来解的。
所以两个非条件概率的题目我们直接用公式来解,并不画图的。



