NO.PZ2018122701000018
问题如下:
The bank’s trading book consists of the following two assets:
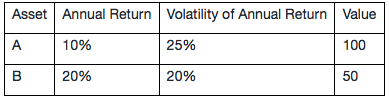
Correlation (A, B) = 0.2
How would the daily VaR at 99% level change if the bank sells $50 worth of asset A and buys $50 worth of asset B?
Assume there are 250 trading days in a year.
选项:
A.$0.2286
B.$0.4776
C.$0.7705
D.$0.7798
解释:
B is correct.
考点Parametric Estimation Approaches
解析The trade will decrease the VaR by 0.4776。
易错点:求daily VaR,但题干给的是annual return。
t=0,组合由$100A+$50B构成,μP =13.33%, 由年转化为天,13.33%/250=0.0533%.
σP =19.15%, 由年转化为天, 19.15%/SQRT(250)=1.2111%
daily 99%VaR=(2.33*1.2111%-0.0533%)*$150=$4.1528
t=1,组合由$50A+$100B构成,μP =16.66%, 由年转化为天,16.66%/250=0.0667%.
σP =17.08%, 由年转化为天, 17.08%/SQRT(250)=1.0801%
daily 99%VaR=(2.33*1.0801%-0.0667%)*$150=$3.6749
所以$4.1528-$3.6749=0.4779,最接近的是B选项。
这一题的思路不太明白,是先求组合的u和σ对吧,组合的u就是各自的权重乘以对应的u相加,但是组合的σ是怎么求出来的呢?然后t分别=0和1,这个又是什么意思?



