NO.PZ2020033002000084
问题如下:
If two bonds each has a face value of $ 50 million and a one-year cumulative default probability of 2% with zero recovery rate. What is its 99.9% credit var with 99.9% confidence level over the next month, assume they are not correlated?
选项:
A.
$0
B.
$0.168million
C.
$49.832million
D.
$99.832million
解释:
C is correct.
考点:Credit VaR
解析:首先算出来月化的PD也就是0.168%,那么expected loss就等于0.168%*100%*(50+50)million=0.168 million。
然后就要算WCL,两只债券违约的情况如下图:
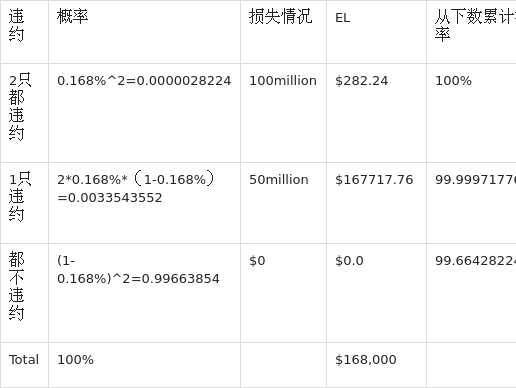
可以看到50million是第一个累计概率超过99.9%的损失,所以WCL就等于50million。
Credit VaR 就是50million-0.168million=49.832million。
最后一列的概率咋算出来的?



