老师您好,我对factor-based strategy中risk management的理解有点模糊,您看我这样理解对么?
首先如果根据统计,我认为有3个factor对return的影响是比较显著的,就可以得到:
Re=a+b1F1+b2F2+b3F3+ε
然后我可以把这3个factor当成是3个股票,根据这3个factor的σ,互相之间的ρ通过最优化求解,类似求马科维茨有效前沿,找到sharp ratio最大的那个点,此时b1 b2 b3的值(相当于权重)理论上就是我要找的最优点
例如此时我得到的结果是 Re=a+1*F1+2*F2+3*F3+ε
最后比如我找到了10只股票,把这10只股票也根据这3个factor进行分解,并通过设置一定的权重使得这10只股票加起来的3个factor的系数等于上面的最优解的系数(就是下图李老师强化班里说的这个过程),此时这10只股票的权重就是我portfolio里资产的最终组合
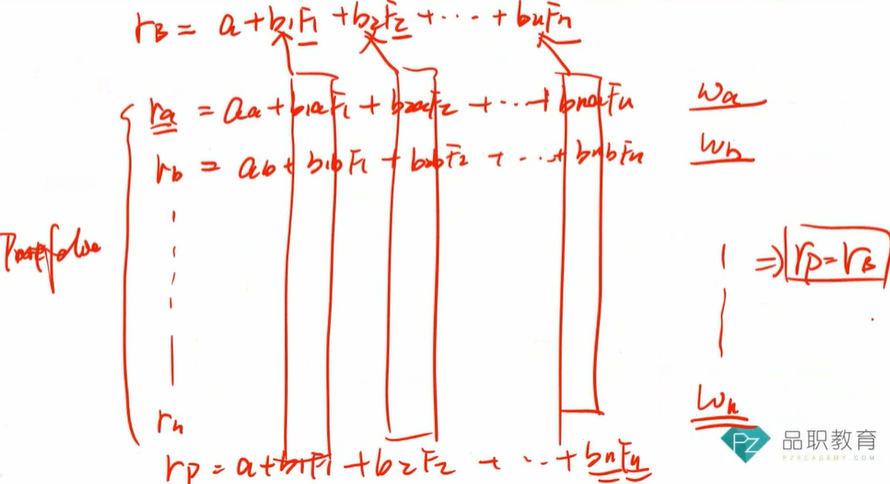
问题主要如下:
1)麻烦老师看一下整个过程是不是我理解的这样?因为知识点是分开的,所以对整个流程不是很清楚
2)在最后一步中,股票的数量应该是不固定吧,比如我用3只股票,30只,300只都可以根据不同的权重凑出最优解的系数,那这一步要怎么样才是最优的?再用一次最优化求解么?感觉太理论了,现实中有这么做的么....
3)这样做的最终结果是不是类似CAPM里面充分分散化之后只承担系统性风险,这样分散化之后相当于只承担了这个3个factor带来的风险,剩下的都分散掉了?如果这三个factor里面不包含系统性风险(Rm),那系统性风险相当于也能被分散掉了?这可能么?还是说如果不包含Rm这个回归方程结果肯定是不显著的,也就是Rm必须是其中一个factor



